fe=l

где I - число действующих па систему возмущений, а (р) = -Wf (р).

Это же выражение может быть получено из операторного уравнения (5.16), еслиоператор дифференцированияр=- положить равным пулю.

Первое слагаемое (8.1) представляет собой составляющую статической ошибки, определяемую задающим воздействием. Эта составляющая, в соответствии с изложенным в § 5.3, может быть отличной от пуля только в следящих системах при статическом регулировании.

Во-вторых, можно основываться на некоторых частотных свойствах рассматриваемой системы, характеризующих ее поведение в установившемся режиме при действии па входе гармонического сигнала. К ним относятся полоса пропускания, относительная высота резонансного пика и др.

Оба эти подхода имеют в настоящее время большое распространение и используются параллельно. И тот и другой подход требует изучения условий эксплуатации построенных систем автоматического регулирования, так как только па основании такого изучения можно правильно сформулировать количественные оценки, которые могут быть использованы в практике проектирования и расчета новых систем.

Связь между временными и частотными свойствами системы автоматического регулирования имеет сложный характер и может быть определена в общем виде только в простейших случаях, например для систем, описываемых дифференциальным уравнением второго порядка.

Однако отсутствие зависимостей, связьпзающих в общей форме свойства системы во временном и частотном представлениях, не может служить препятствием для развития и независимого использования критериев качества того или иного направления.

Использование того или иного подхода при формулировании критериев качества определяется в настоящее время удобствами его применения в системах конкретного вида, а также, в известной мере, сложившимися в данной области традициями,

§ 8.2. Точность в типовых режимах

Для оценки точности системы регулирования используется величина ошибки в различных типовых режимах. Ниже будут рассмотрены наиболее употребительные режимы.

1. Неподвижное состояние. В качестве типового режима рассматривается установившееся состояние при постоянных значениях задающего и возмущающего воздействий. Ошибка системы в зтом случае называется апатической. Величина ошибки может быть найдена из общего выражения (5.2). Для этого необходимо положить g (t) = g = const. Далее необходимо учесть действующие на систему возмущенрш. В общем случае их может быть несколько: /i (t), /2 (t) и т. д. Тогда в правой части (5.2) появится несколько слагаемых, определяемых имеющимися возмущениями. В неподвижном состоянии необходимо положить fi (t) = = const, /2 (t) = /20 = = const и т. д. Затем можно использовать изображения функций по Лапласу или Карсону - Хевисайду. Используем, например, изображения Карсона - Хевисайда. Тогда изображение постоянной величины равно ей самой, т. е. G (р) - go, Fi (р) = /ю, Fip) = /20 и т. д. Далее необходимо воспользоваться теоремой предельного перехода и получить установившееся значение ошибки (статическую ошибку):

в статических системах W (0) = &%редставляет собой общий коэффициент усиления по разомкнутой цепи. Вэтом случае первое слагаемое (8.1) может быть представлено в виде

Однако эта составляющая ошибки практически всегда может быть сведена к нулю посредством использования неединичной обратной связи или путем масштабирования задающего воздействия или регулируемой величины (см. § 9.3).

При астатическом регулировании W (0) ->- сю. Поэтому первая составляющая (8 1) обращается в нуль.

В системах стабилизации g (t) ~- О, что также обращает в нуль хс. В связи с этим практически во всех случаях первая составляющая статической ошибки может быть принята равной нулю.

Второе слагаемое (8.1) никогда не обращается в нуль, так как даже использование регулирования с астатизмом высокого порядка и использование принципа регулирования по возмущению (см. § 9.2) могут обратить в нуль лишь часть слагаемых, находящихся под знаком суммы (8.1).

При выводе выражения (8.1) предполагалось, что чувствительный элемент, определяющий разность между требуемым и действительным значениями регулируемой величины, является идеальным и определяет имеющуюся ошибку в соответствии с выражением х (t) = g (t) - у (t). В действительности чувствительному элементу как измерительному органу присущи свои ошибки. Ошибку чувствительного элемента можно рассматривать также как некоторое возмущающее воздействие и считать, что она входит во второе слагаемое (8.1). Однако на практике удобнее эту ошибку учитывать отдельно и считать, что статическая ошибка равна (при = 0)

Хст = Xci -\- Хст, (8.3)

где Жст представляет собой второе слагаемое в выражении (8.1) и определяется внешними возмущениями, х является ошибкой чувствительного злемента.

Рассмотрим теперь ошибку регулирования Жст- Примем для простоты, что на систему действует одно возмущающее воздействие Z. Тогда в статической системе получим

В этом равенстве представляет собой отношение установившейся ошибки к постоянному возмущению (коэффициент статизма) в системе с разомкнутой цепью регулирования. Эта же величина, деленная на 1 К, соответствует коэффициенту статизма в замкнутой системе регулирования. Величина I К, по сути дела, показывает эффективность регулирования с точки зрения уменьшения установившейся ошибки.

В астатической системе W (0) оо. Однако это еще не означает, что ат == О, так как возможен случай, когда (0) ->- оо. Вследствие этого для каждого действующего на систему возмущения необходимо определить факт наличия или отсутствия установившейся ошибки посредством нахождения значения (8.4).

Для иллюстрации этого на рис. 8.1 изображена структурная схема системы автоматического регулирования. Она содержит объект с передаточной функцией Wo (р) и астатический регулятор с передаточной функцией к

(р) - Пусть объект не имеет интегрирующих свойств и Wo (0) = ко.

На систему действуют два возмущения -Д и f. В разомкнутой системе (как показано па рис. 8.1)

г hr.

и в замкнутой

Wo (Р)

ii+h

где W ij)) = Wo (р) W-p (р) - передаточная функция разомкнутой системы.

Отсюда по теореме предельного перехода определяем установившуюся ошибку, положив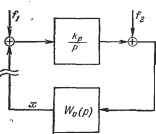

Рис. 8.1.

Таким образом, первое возмущение дает статическую ошибку, а второе не дает. Из рассмотрения рис. 8.1 видно, что возмущение /i приложено до интегрирующего звена, а /а - после. Из этого и вытекает правило, по которому можно определить, устраняет ли астатический закон регулирования статическую ошибку от какого-либо возмущения. Для вьшолнепия этого необходимо, чтобы интегрирующий зле-мент был включен в цепь регулирования до места приложения данного возмущения. Это объясняет, в частности, тот факт, что включение интегрирующих элементов и повышение степени астатизма не дает возможности устранить ошибку чувствительного злемента х, которую можно рассматривать как возмущение.

2. Движение с постоянной скоростью. В качестве второго типового режима используется режим движения системы с постоянной скоростью V = const, который будет наблюдаться в установившемся состоянии при задающем воздействии, изменяющемся по закону g (t) = vt, где v = const, и при постоянных значениях возмущающих воздействий /i (t) = /ю, /г (t) = = /20 и т. д. Этот режим имеет смысл только в следящих системах и системах программного регулирования.

Используя изображения Карсона - Хевисайда, в этом случае получаем G{p) =-у. Flip) = /10, F (р) = /20 и т. д.

Из общего выражения для ошибки (5.16) посредством теоремы о пре-

дельном переходе может быть найдена установившаяся ошибка в этом режиме:

Хуст -

rWu (р) ho

i+W(p) }р-.о L i + W(p) J

р- 0

(8.5)

Второе слагаемое этого выражения дает статическую ошибку (при условии, что возмущающие воздействия такие же, как в неподвижном положении системы), в которой может быть также учтена ошибка чувствительного элемента.

Первое слагаемое (8.5) имеет смысл только при астатизме первого порядка, т. е. в том случае, когда передаточная функция разомкнутой системы может быть представлена в виде (5.42)

W (т,\ (1+Дт-1Р+ +ВоР)