Обратимся теперь к электронным моделям матричного типа. На рис. 7.11 изображена упрощенная структурная схема такой модели, позволяющей исследовать дифференциальные уравнения не выше третьего порядка (третий

порядок принят только для облегчения изложения).

Три операционных усилителя 1, 2 ш 3, работающих в режиме интегрирования, включены так, что все выходы соединяются со входами всех усилителей через делители с соответствующими коэффициентами передачи (оц, 215 031 и т. д.). Кроме того, через делители правых частей уравнения (а, а, и на входы усилителей от генераторов функций времени поступают воздействия на систему (т), F, (т) и F (т). В соответствии со свойствами операционных усилителей, работающих в режиме интегрирования, изображенная на рис. 7.10 структура описывается системой уравнений, записанных для машинных переменных.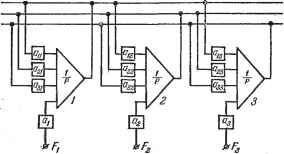

Рис. 7.11.

+ 1Д1 + а А + 313 + (т) = О, + aiXi + 222 + 32X3 -f aF (т) = О,

-Ь 131 + 23X2 + 333 + 33 (т) = 0.

(7.73).

К такому виду и должны приводиться уравнения, описывающие реальный объект. После получения системы уравнений (7.73) остается установить на делителях соответствующие значения коэффициентов, и задача оказывается набранной на модели.

Если исследуемая система определяется одним уравнением третьего порядка, записанным для машинных переменных.

A2+A,X, = F{x),

(7.74)

то переход к системе (7.73) делается введением вспомогательных функций

Х2=-

dx dX.

у ал2 dXj

Тогда вместо (7.74) получим систему уравнений

(7.75)

-Х, = 0,

dXs Y п -h AiXs + AA + AsX ~F{r) = 0.

(7.76)

Эта система уравнений является частным случаем системы (7.73) и может быть набрана на рассматриваемой электронной модели (рис. 7.11).

Электронная модель матричного типа ЭЛИ-14 работает примерно по описанному выше принципу, но содержит не три, а шесть интеграторов, что позволяет набрать на ней систему из шести дифференциальных уравнений первого порядка типа (7.73) или одно дифференциальное уравнение шестого порядка.

Все, что было рассмотрено выше, относится к моделированию линейных дифференциальных уравнений с постоянными коэффициентами. При необходимости исследовать процессы в системах с переменными коэффициентами или в системах с временным запаздыванием к линейной электронной модели добавляются соответственно блоки переменных коэффициентов и блоки временного запаздывания. Добавление нелинейных блоков позволяет исследовать процессы в нелинейных системах. Все эти добавочные блоки существенно повышают эффективность электронных моделей, так как позволяют сравнительно просто и достаточно точно исследовать процессы в сложных нелинейных и особых линейных системах, что является в большинстве случаев недоступным для аналитических методов расчета.

Электромеханические модели. Существующие электронные вычислительные машины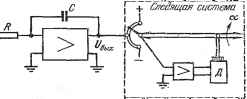

имеют следующие недостатки, которые в некоторых случаях затрудняют их использование.

1. Сложность сопряжения с реальной аппаратурой вследствие того, что выходной величи- Рис. 7.12. ной электрической модели всегда является напряжение постоянного тока, а входные величины в реальной аппаратуре могут быть самыми различными (напряжение переменного тока, угол поворота, перемещение, угловая или линейная скорость и т. д.). Это требует использования в электронных моделях специальных преобразователей выходного напряжения, которые ухудшают точность и динамические характеристики электронных моделей.

2. Трудность воспроизведения в электронных моделях сложных нелинейных зависимостей, таких, например, как тригонометрические функции, функции двух переменных, произведение нескольких величин и т. п.

3. Ограниченность допустимого времени работы электронных интеграторов. Это время не превосходит нескольких сотен секунд, что ограничивает возможности работы модели в сопряжении с реальной аппаратурой, где не может использоваться изменение масштаба времени.

Чтобы избавиться от этих недостатков, для некоторых задач используются электромеханические модели. В настоящее время существует два способа построения таких моделей.

Первый способ заключается в том, что в модели используется интегратор (рис. 7.12), состоящий из операционного интегрирующего усилителя и вспомогательной следящей системы, преобразующей напряжение постоянного тока С/бых на выходе электронного интегратора в угол поворота а следящей системы. На базе такого интегратора и может быть построена электромеханическая модель исследуемой системы. В этой модели могут быть использованы электронные операционные усилители в режиме масштабирования, инвертирования и суммирования, а также электронные модели типичных нелинейностей, построенные на диодных элементах.

Однако то обстоятельство, что выходные величины интеграторов представляют собой углы поворотов некоторых механических валиков, позволяет

Рис. 7.13.

Если электромеханическая модель строится на базе интегрирующего привода постоянного тока, то в ней могут быть использованы те же элементы, что и в описанной выше модели, построенной на базе электронного интегратора с преобразующей следящей системой.

значительно легче решать вопросы сопряжения с реальной аппаратурой, поскольку на этих валиках легко могут быть установлены требуемые датчики (датчики угла или перемещения, датчики угловой скорости и т. п.). Кроме того, это же обстоятельство позволяет сравнительно просто учитывать в исследуемой системе сложные нелинейные зависимости, что делается установкой на выходных валиках интеграторов таких элементов, как синусно-косинус-ные потенциометры, функциональные потенциометры, эксцентрики для воспроизведения функции одной переменной, коноиды для воспроизведения функций двух переменных, множительные и делительные устройства и т. п.

Набор задачи на электромеханической модели делается примерно так же, как и на электронной, с учетом специфики тех новых элементов, которые

используются для установки на выходных валиках интеграторов.

На подобном принципе работает, например, электромеханическая мо-дель типа Электрон . Электромеханические модели подобного типа особенно удобны для моделирования пространственного движения самолетов, ракет, космических кораблей, подводных лодок [и т. д. Однако в этих моделях по-прежнему существует ограничение времени их непрерывной работы, что связано с наличием электронного интегратора.

Некоторым их недостатком, который свойствен вообще всем электромеханическим моделям, является то, что следящая система преобразования выходного напряжения электронного интегратора в угол поворота выходного валика вносит нежелательный динамический эффект, связанный с введением в модель передаточной функции самой следящей системы. Эта передаточная функция может быть обычно сведена к передаточной функции апериодического звена первого порядка или передаточной функции колебательного звена.

Второй способ построения электромеханических моделей заключается Б том, что электронный интегратор исключается, а интегрирование ведется на интегрирующем приводе [10], схема которого изображена на рис. 7.13. В качестве входной величины здесь может быть напряжение постоянного или переменного тока. Это напряжение сравнивается с напряжением тахогенератора У/ постоянного или, соответственно, переменного тока, который установлен на оси исполнительного двигателя Д. Если коэффициент усиления усилителя достаточно велик, то напряжение тахогенератора с большой точностью будет равно входному напряжению JJ = С/вх- Так как напряжение тахогенератора с большой степенью точности пропорционально скорости его вращения, то, следовательно, можно записать зависимость

= Штг = Швх. (7.77)

Угол поворота выходного валика оказывается пропорциональным интегралу от входного напряжения:

Vdt. (7.78)