Знак минус в формуле (7.58) показывает, что операционный усилитель инвертирует входной сигнал (меняет его знак). Это связано с установкой в усилителе нечетного числа каскадов.

Рассмотрим три основных режима работы усилителя.

1. При Zg (р) = и Zi (р) = Ri усилитель выполняет функцию умножения входной величины на постоянный множитель (рис. 7.6, а):

ip) = {р) == ~hU,

Лр)-

(7.59)

--Bxv/y-----

Упрощенное изображение такого усилителя показано на рис. 7.6, а справа.

2. При Zq (/?)=- , что соответствует установке в цепи обратной связи

конденсатора, ш Zi (р) = R усилитель работает в режиме интегрирования

входной величины (рис. 7.6, б):

>

tBbix ip) =

t/Bx(p) =

= -t/Bx(p).

(7.60)

>

11 Hb

Два варианта упрощенного изображения такого усилителя I-ц-. изображены на рис. 7.6, б К, справа.

/? i - L11£J />- 3. При Zo = R ш Ziip) =

= -у;, ЧТО соответствует уста-

новке конденсатора во входной цепи, усилитель работает в режиме дифференцирования (рис. 7.6, в):

г7вых(р)=~адг7вх(р) =

= ~kspU{p)- (7-61)

Упрощенное изображение такого усилителя показано на рис. 7.6, в справа. Рис. 7.6. Режим дифференцирования

обычно не используют при моделировании, так как в этом режиме сильно возрастает влияние высокочастотных помех и наводок.

На рис. 7.7 изображен операционный усилитель в режиме суммирования. Как нетрудно показать, при Zq (р) = Rq

>

С/вых(р)=-?о2

Свх г (Р)

(7.62)

При Zo(j)) = получаем суммирующий интегрирующий усилитель.

В табл. 7.3 приведены типичные случаи использования операционного усилителя для получения различных динамических звеньев.

В таблице использован мащинный оператор дифференцирования

й% mi dt

(7.63)

При моделировании в натуральном масштабе времени х = t ж Р = р.

>

Рис. 7.7.

Электроньая модель структурного типа имеет в своем составе несколько операционных усилителей, которые могут работать в режиме интегрирования, т. е. с конденсатором в цепи обратной связи. Число этих усилителей определяет наивысший порядок дифференциального уравнения, которое может быть исследовано на данной модели. Кроме того, имеется ряд вспомогательных усилителей, при помон],и которых можно осун],ествлять операции умножения на постоянный множитель (масштабирование), перемены знака (инвертирование) и суммирования.

Исследуемые процессы в виде изменения мапшнных переменных (напряжений) могут наблюдаться и фиксироваться при помощи электронных и магнитоэлектрических осциллографов.

Для приложения к электронной модели исследуемой системы задающих и возмущающих воздействий используются генераторы, которые могут воспроизводить требуемые функции времени, например линейную функцию, синусоиду, экспоненту, прямоугольную или треугольную волну и т. п., в виде соответствующего изменения электрического напряжения. Существуют также генераторы случайных а) величин, например генераторы шу-

мового напряжения.

Кроме того, электронная модель имеет ряд вспомогательных устройств, позволяющих после набора исследуемой задачи производить пуск и остановку решения дифференциальных уравнений, фиксацию решения в заданной точке, периодизацию решения и т. п.

Набор задачи на электронной модели структурного типа может быть осуществлен двумя способами:

1) по дифференциальному уравнению, которым описывается исследуемая система,

2) по структурной схеме исследуемой системы.

Рис. 7.8. Рассмотрим порядок набора

задачи на простейшем примере. Начнем с первого способа. Пусть дана система регулирования, структурная схема которой представлена на рис. 7.8, а. Для этой схемы передаточная функция разомкнутой системы

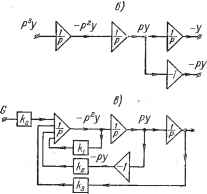Н осциллограсру

(7.64)

Дифференциальное уравнение замкнутой системы, записанное в символической форме, в соответствии с (5.15) будет

II + (Р)] v{t) = W (р) g (t), где у (t) - регулируемая величина, а g (t) - задающее воздействие.

Таблица 7.3

Типовые динамические звенья электронных моделей

Схема

Передаточная функция

1>

W{P)=-, TRC

\-\-TP

rlH=i,

T\ = Rfi, T2, = R2C

W{P)=-k

Ti==RiC

В рассматриваемом случае, учитывая (7.64), получим

(йоР + iP + аР + з) it) = 3 (О (7.65)

ао = ГхГз, 1 = + Га, 2 = 1 и 3 == fejun

Перейдем к машинным переменным Y /ггу и G - Wge- Учитывая соотношения т = mtt ш р - mtP, получим из (7.65) дифференциальное уравнение для машинных переменных!

{АР + АР + ЛР + 4з) Г (т) = (т), (7.66)

-Тде Ао = ( 0 ti -а = ( 2. = з И == -