Если на вход поступает сигнал типа единичной ступенчатой функции Xi{t) = i{t), изображение которого по Лапласу равно [Х (р) = , то изображение выходной величины будет

Это изображение имеет однократный полюс в начале координат {pi = 0), Если на вход системы поступает сигнал типа (t) = vt-l (t), изображение которого Xl (р) = , то изображение вьпсодной величины будет иметь

в начале координат двукратный полюс (pi = р = 0).

В связи с этим для использования интегральной зависимости (7.45) необходимо отделить от изображения Фурье искомой функции времени длены, содержащие полюсы на мнимой оси.

Рассмотрим частный случай, когда изображение Карсона - Хевисайда Ф (р) = рХ (р) не имеет полюсов на мнимой оси. К этому случаю сводится, например, задача нахождения переходной функции в устойчивой системе, если даны, ее передаточная функция Ф (р), не имеющая полюсов на мнимой

оси, и входное воздействие типа единичной ступенчатой функции G (р) =-

Тогда изображение по Лапласу выходной величины будет

Yip)==

и соответственно ф (р) = рУ (р) = Ф (р).

Тогда оказывается, что частотное изображение ф (ja) совпадает с частотной передаточной функцией замкнутой системы Ф (jco), а вещественная Рф(со) и мнимая <5ф(со) части в формуле (7.46) совпадают с вещественной Р (со) и мнимой S (оз) частотными характеристиками замкнутой системы. К аналогичному результату можно прийти, если рассматривать реакцию системы на скачок внепшего возмущения. Тогда вещественная и мнимая части в формуле (7.46) будут совпадать с вещественной и мнимой частями частотной передаточной функции по возмущению Ф. (/со) = Рр (со) + jSp (со).

К тому же частному случаю могут сводиться и другие задачи исследования переходных процессов в системах регулирования, например нахождение ощибки системы при приложении скачкообразного внещнего возмущения, нахождение функции веса системы и др.

В этом случае существует ограниченное установившееся значение искомой функции времени х (t), которое можно получить, подставляя в ф (р) значение р = 0.

Учитывая, что <5ф(0) = О, получаем Жут = ф (0) = Pq, (0). Тогда подынтегральная функция (7.45) может иметь однократный полюс в начале координат. Его можно устранить, рассматривая не саму величину х (t), а разность-X (t) - Хуст = X (t) - P<f (0), которой соответствует разность изображений Ф (р)- ф (0) = Ф (р) - Рф(О). В результате приходим к следующей интегральной зависимости:

- со

Используем формулу Эйлера

Подставляя последнее выражение в (7.47), используя формулу (7.46) и отбра- рывая мнимую часть, которая должна быть равной нулю, так как функция

0 = -

Рф(0) 1 f Pv(<o)sincof , 1 -S-+1Г

5ф (о) cos со<

-dco. (7.50)

Совместное решение (7.49) и (7.50) дает два выражения для нахождения искомой функции времени:

9 Т в> (ш) COS (oi it) = PAO) + i ] -d, (7.51)

? с /n,(tu)sm(ui

(*)=--1-Ч- ( 2>

причем (0) = Жуст

Таким образом, можно отыскать оригинал х {t) по известной вещественной (со) или известной мнимой (оз) частям частотного изображения ф (/ ) = jaX (/со). Обычно для этих целей используется вещественная часть изображения Pq, (со).

Если входное воздействие представляет собой единичный скачок, то как указывалось выше, частотное изображение ф (/со) совпадает с частотной передаточной функцией замкнутой системы Ф (/оз). Тогда в формулы (7.51) и (7.52) будут входить вещественная и мнимая части частотной передаточной функции замкнутой системы Ф (/оз) = Р (оз) + jS (со). Следовательно, в этом случае для построения переходного процесса, который будет представлять собой переходную функцию системы h (t), необходимо в формуле (7.52) положить Рф (со) = Р (оз), где Р (оз) - вещественная характеристика системы. В результате получим

x{t) = h{t)= FZHidco. (7.53)

Аналогичным образом, при нахождении реакции системы на единичный скачок возмущающего воздействия необходимо использовать вещественную часть частотной передаточной функции по возмущению.

В дальнейшем изложении будем иметь в виду случай, определяемый формулой (7.53), хотя методика построения переходного процесса остается единой и для общего случая (7.52).j

X (t) является, конечно, вещественной, получаем

{t)- (0) = i- J ----dco. (7.48>

- оо

Подынтегральное выражение представляет собой четную функцию частоты. Поэтому интегрирование по всем частотам можно заменить интегрирова- нием только по положительным частотам, а затем удвоить результат.

Так как

1 Р Рф(0)8ШШ< Рф(0)

1Г] -S-dco=-,

то в результате имеем

... ф(О) , 1 f (со) sin (Of 1 f gq>((u)C0SOf

Если принять нулевые начальные условия, то до приложения внещнего воздействия (при t <iO) х {t) = 0. Заменив в (7.49) время на -t, получим

Интегрирование выражения (7.53) представляет большие трудности. Поэтому обычно используется приближенное решение задачи. Для этой

цели вводится понятие типовой единичной трапецеидальной вещественной характеристики (рис. 7.3).

Единичная трапеция имеет высоту, равную единице и частоту среза озц? также равную единице, точнее, 1 сек~.

Единичная трапеция характеризуется частотой излома, которая может быть задана в виде коэффициента наклона трапеции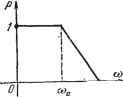

со =/ /сек

Рис. 7.3.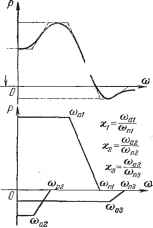

Для единичных трапеций с различными коэффициентами наклона по выражению (7.53) может быть вычислен оригинал, т. е. функция времени. Эта функция получила название /j-функции. В настоящее время составлены подробные таблицы /j-функции для различных коэффициентов наклона, лежащих в пределах О < X < 1 (см. приложение 1).

По такой таблице для каждого коэффициента наклона единичной трапеции может быть построена функция времени h (t), где t- безразмерное вре- рщ мя, соответствующее единичной трапецеидальной характеристике.

Метод построения кривой переходного процесса заключается в том, что построенную вещественную характеристику исследуемой системы (рис. 7.4) разбивают на ряд трапеций, заменяя приближенно кривые линии прямолинейными отрезками так, чтобы при сложении ординат всех трапеций получилась исходиая характеристика. Затем для каждой трапеции определяется коэффициент наклона. При известном коэффициенте наклона по таблицам могут быть построены h-функции для каждой трапеции.

Кривая переходного процесса может быть получена суммированием построенных /j-функций

с учетом правил масштабов. Правила масштабов заключаются в следующем.

1. Перед сложением ординаты каждой Л-функции необходимо умножить на высоту соответствующей трапеции (см. рис. 7.4), так как Л-функция построена для трапеции, имеющей единичную высоту. При этом необходимо учитывать знак высоты, считая высоту положительной для трапеций, расположенных вьппе абсцисс.

3. Перед сложением необходимо изменить масштаб времени каждой /j-функции, так как Л-функции построены для единичной трапеции, имеющей частоту среза озц = 1 сек~. Изменение масштаба времени делается в соответствии с теоремой подобия (табл. 7.2).

Действительное время равно времени t, приведенному в таблице й-функ-ций, деленному на частоту среза соответствующей трапецеидальной характеристики:

При нахождении реакции системы на единичную импульсную входную функцию, т. е. функции веса w {t), можно пользоваться общей формулой

Рис. 7.4.