устойчивого или нейтрально-устойчивого в разомкнутом состоянии одного изолированного канала не будет охватывать точек комплексной плоскости, соответствующих и К-

Колебательная граница устойчивости будет иметь место, если вьшол-няется одно из равенств: Wo (/ ) = К или Wo (/ ) = % .

Из (6.41) нетрудно видеть, что при а = О обе точки стягиваются в одну точку K-i = = - 1 iTO соответствует обычной формулировке критерия Найквиста.

Другой метод расчета устойчивости заключается в том, что вводятся в рассмотрение комплексные величины

г/* = г/1+/г/2,

Матричная зависимость (6.38) дает два равенства:

г/1 = Wo (р) Xi + aWo (р) х, I У2= -aWoip) Xi+Woip) х. j

(6.42)

(6.43)

Умножая второе равенство на / и складывая, получаем для комплексных величин

у* = (1 /а) Wo (р) X* = W ip) X*. (6.44)

Здесь введена эквивалентная передаточная функция разомкнутой двумерной системы

Иэ (Р) = (1 - ja) Wo ip).

(6.45)

Для дальнейшего расчета может использоваться критерий Найквиста в своей обычной формулировке. Однако при построении а. ф. х. частотной

ш>0

ImWgQw)

ReWg(ja))

а>0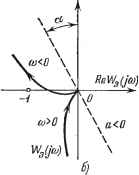

Рис. 6.30.

передаточной функции Wg (/о) она оказывается повернутой по сравнению с исходной а. ф. X. величины Wo (/со) по часовой стрелке на угол а = arctg а. Это соответствует введению дополнительного фазового сдвига, что приближает а.ф.х. к точке (-1, /0) и снижает запас устойчивости (рис. 6.30, й). Кроме того, mod W (/со) оказывается в ]/1 + раз больше mod Wq (/со), что также способствует снижению запаса устойчивости.

При а < О поворот а. ф. х. будет против часовой стрелки и к точке (-1, /0) будет приближаться верхняя ветвь а. ф. х., соответствующая отри-

цательным частотам (рис. 6.30, б). Это также соответствует снижению запаса устойчивости.

Заметим, что и в слзчае перехода к комплексньтм величинам у* и х* можно произвести расчет по а. ф. х. исходной одноканальной системы Wq (/со). В зтом случае колебательная граница устойчивости будет при выполнении условия

(/со) = (1 - /а) Wo (/со) = -1. (6.46)

Условие (6.46) сводится к равенству

о(--) = Т=-Т-/Т-ь (6.47)

что согласуется с первым методом расчета устойчивости.

Рассмотренпые методы позволяют упростить определение устойчивости двумерной системы по сравнению с использованием результируювего характеристического зфавнения (6.39), так как требзют рассмотрения передаточной функции Wq (р) одного изолированного канала.

ГЛАВА 7

ПОСТРОЕНИЕ КРИВОЙ ПЕРЕХОДНОГО ПРОЦЕССА В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

§ 7.1. Общие соображения

Дифференциальное уравнение обыкновенной линейной системы автоматического регулирования, записанное для ошибки регулирования, согласно (5.2) имеет вид

D {р) x{t)Q{p)g it) +N{p)f it), (7.1)

где P = -- алгебраизированный оператор дифференцирования, g (t) -

задающее воздействие и / (f) - возмущающее воздействие.

Решение линейного дифференциального уравнения с постоянными коэффициентами (7.1) будет

X (t) = х {t) + х (О, (7.2)

где Жп (t) - общее решение однородного уравнения D (р) х (t) = О, имеющее вид

п = Ci + Се + . . . + СУгг\ (7.3)

причем Cj, . . ., Cji - произвольные постоянные, определяемые из начальных условий процесса, а р, . . ., р - корни характеристического уравнения D (р) = 0. Выражение (7.3) заьисано для случая отсутствия нулевых и кратных корней.

Частное, или вынужденное решение х (t) определяется правой частью уравнения (7.1), и оно соответствует некоторому установившемуся режиму в системе, который будет существовать после затухания х (t).

Полным решением (7.2) описывается процесс регулирования в линейной системе (общий случай возмущенного движения системы). Первая часть этого решения х (t) в виде (7.3) представляет собой собственное движение систе мы, наложенное на частное решение ж (t).

Исходное дифференциальное уравнение системы может быть записано также для регулируемой величины у (t) = g (t) - х {t). В системах стабилизации g (г) = О и поэтому у {t) = - X {t).

Необходимо обратить внимание на следующее важное обстоятельство. Частное решение х {t) складывается из отдельных слагаемых, отвечающих отдельным членам правой части дифференциального уравнения (7.1). Если действует несколько возмущающих воздействий, то в решении будет соответственно и несколько слагаемых. При этом каждое слагаемое частного решения х (t) может определяться по отдельности для каждого возмущающего или задающего воздействия независимо от других, а затем их можно складывать. В этом состоит так называемый принцип суперпозиции.

Следовательно, если имеется дифференциальное уравнение

D{p)x{t) = Q{p)g {t) + Nj, (р) и it) + ip) и it).