КРИТЕРИИ устойчивости

[ГЛ. 6

Сделаем теперь два замечания, касающихся использования для определения устойчивости замкнутой системы передаточной функции разомкнутой системы.

Замечание 1. В случае многоконтурной системы регулирования размыкание ее для получения передаточной функции разомкнутой системы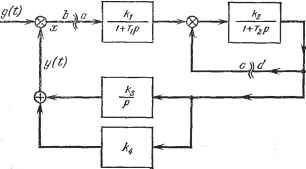

Рис. 6.24.

можно делать, вообще говоря, в произвольном месте. Рассмотрим, например, систему, структурная схема которой изображена на рис. 6.24.

Разомкнем систему на входе первого звена. Тогда, рассматривая точку а как вход, а точку Ъ как выход, получаем передаточную функцию разоапшу-той системы

W-i + yp 1 + /2 + Г2Р \ Р Ч P(l+riP)(l + + y2P)

Разомкнем теперь ту же систему не на входе первого звена, а в цепи обратной связи второго звена (точка с соответствует входу, а точка d - выходу).

Передаточная функция разомкнутой системы в этом случае

2P(l+?lP)

W (р) = .

1±I?P

P (l + lP) {i+T2P) + kik2k3-\-kik2kp

l + fiP l + aP

Передаточные функции W (p) и W (p) получились различными. Однако им соответствует одно и то же характеристическое уравнение замкнутой системы I -\- W (р) = i -\- W (р) = О, которое имеет вид

TiTp + (Ti +Г2 -\-:hTy)p + (i-\rk2 + кфК) Р + hKK = 0.

Поэтому для определения устойчивости можно пользоваться передаточной функцией разомкнутой системы, полученной размыканием исходной системы в произвольной точке, в которой выполняется условие детектирования.

Однако передаточные функции W (р) и W (р) имеют различие. Только передаточная функция W (р) связывает между собой изображения регулируемой величины и ошибки, и только она связана с передаточной функцией замкнутой системы Ф (р) известным соотношением (5.26):

- Ф (Р)

H7(p)=.-ZM.

1-Ф(р)

Передаточную функцию при размыкании на входе первого звена в дальнейшем будем считать главной передаточной функцией разомкнутой системы

Ж именно ее иметь в виду при рассмотрении методов определения качества регулирования и синтеза систем регулирования.

Замечание 2. При определении устойчивости в используемой передаточной функции разомкнутой системы можно перемещать члены знаменателя в числитель и наоборот, за исключением старшего члена знаменателя. Так, например, если имеется передаточная функция

Wip)--

с0/--с1/--с2/--Сз

ТО для расчета устойчивости она может быть заменена функцией

сорз

В справедливости этого нетрудно убедиться на основании того, что характеристическое уравнение замкнутой системы 1 + W (р) = i + W (р) = О сохраняет при этом свой вид:

СоР + Cip + {bo + С2)р -f bi -f Сз = 0.

§ 6.6. Определение устойчивости по логарифмическим частотным характеристикам

Для определения устойчивости по критерию Найквиста можно строить не амплитудно-фазовую характеристику, а логарифмическую амплитудную частотную характеристику (л. а. х.) и логарифмическую фазовую частотную характеристику (л. ф. х.) разомкнутой системы.

Построение л. а. х. производится по выражению

L (со) = 20 Ig Л (со) = 20 Ig I PF (/со) ,

где А (ci)) - модуль частотной передаточной функции разомкнутой системы (6.29).

Построение л. ф. х. производится по значению я}) (со) частотной передаточной функции (6.29).Для построения л. а. X. ил. ф. х. удобно использовать стандартную сетку, изображенную на рис. 4.10.

Наиболее простое построение получается, если передаточную функцию разомкнутой системы можно свести к виду

W{P) = .-.

[J (i + TiP)

i=i

При подстановке p = /со получаем

L ( ) = 20 Ig 1 -. (6.34)

Фаза (аргумент) частотной передаточной функции

гр (со) = -r.90°-j- S arctgorj- S arctgofj. (6.35)

i=l i=l

На основании (6.34) и (6.35) моншо легко, без дополнительных вьшисле-ний построить асимптотическую л. а. х., для чего на стандартной ceTKe (рис. 6.25) наносятся вертикальные прямые при сопрягающих частотах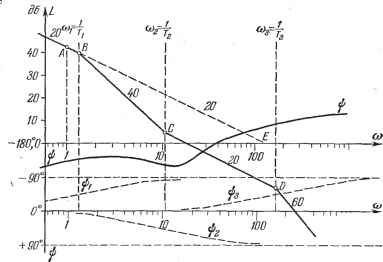

ЮОО Усек

ЮОО /сек

Рис. 6.25.

(i)j=YT и с)г = -уг-. Для определенности построения возьмем передаточнуго функцию разомкнутой системы с астатизмом первого порядка в виде

W{p)

Д (1 + Г2Р)

р(1 + Г1р)(1+ГзрР

которой соответствует выражение для модуля в логарифмических единицах

L = 201g

(6.36)

Примем, что выполняется условие Ti> Т> Tg. Тогда для сопрягающих частот (рис. 6.25) будет выполнено условие Oj <С ©g < №3.

Построение асимптотической л. а. х. начинается с области низких частот. Если частота меньше первой сопрягающей частоты: со < со, то выражение (6.36) приобретает вид

L(co)

которому соответствует прямая с отрицательным наклоном 20 дб/дек, проходящая через точку А с координатами со = 1 сек , L (<а) = 20 Ig К и через точку Е с координатами со = К, L (со) = 0. Эту прямую (первую асимптоту) необходимо провести в низкочастотной области до первой сопрягающей частоты (точка S). Если эта сопрягающая частота соответствует постоянной времени, находящейся в знаменателе (6.34), то необходимо изломать л. а. х. на 20 дб/дек вниз, т. е. провести следующую асимптоту с наклоном, большим на 20 дб/дек. Если зта сопрягающая частота соответствует постоянной времени, находящейся в числителе (6.34), то соответственно необходимо изломать л. а. X. на 20 дб/дек вверх.

В соответствии с выражением (6.36) для рассматриваемого примера в точке В необходимо изломать л. а. х. на 20 дб/дек вниз, в точке С -на