при изменении частоты от -оо до +00 конец вектора W (/и) поворачивался вокруг точки (-1, /0) на угол I 2п против часовой стрелки. Нетрудно видеть, что формулировка критерия Найквиста для случая, когда 1 = 6, вытекает отсюда как частный случай.

Таким образом, при использовании критерия Найквиста, вообще говоря, необходимо убедиться в том, имеются ли в знаменателе передаточной функции разомкнутой системы корни, лежащие в правой полуплоскости, и сколько имеется таких корней.

Если в системе имеются местные обратные связи, например, такого типа, как это изображено на рис. 5.7, то необходимо убедиться в том, что по цепи местной обратной связи не нарушена устойчивость при разомкнутой главной обратной связи. Проверка устойчивости по цепи местной обратной связи может быть сделана посредством использования любых критериев устойчивости, в том числе и посредством кри-терия Найквиста, который может применяться для разомкнутой местной обратной связи обычным путем построе- р ния для этой цели, амплитудно-фазовой характеристики.

В случае, если для местной обратной связи будет получено указание на ее неустойчивость, необходимо -у- определить число корней, лежащих в правой полуплоскости.

Следует заметить, что, хотя теоретически вся система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи, практически такой случай является нежелательным и его Рис. 6.21.

надо избегать, стремясь использовать только устойчивые местные обратные связи. Это объясняется наличием некоторых нежелательных свойств, в частности появлением условной устойчивости, которая при имеющихся обычно в системе нелинейностях может в некоторых режимах привести к потере устойчивости и появлению автоколебаний. Поэтому, как правило, при расчете системы выбирают такие местные обратные связи, которые были бы устойчивыми при разомкнутой главной обратной связи.

Знаменатель передаточной функции разомкнутой системы (6.28) может иметь чисто мнимые корни. Пусть, например, имеется один нулевой корень Pi = О, пара мнимых корней Рг, з == ± /Р) а все остальные корни знаменателя Q (р) лежат в левой полуплоскости (рис. 6.21).

Передаточную функцию разомкнутой системы в этом случае можно представить в виде

<?(Р) (P-fP)<?o(P) Р + Р

Для устранения неопределенности при изменении частоты от -оо до --оо можно использовать изложенный выше прием и отнести три корня, лежащих на мнимой оси, к левой полуплоскости, обойдя их справа по полуокружностям бесконечно малого радиуса.

В этом случае на частотах (в=Ои(й = ±р модуль W (/со) будет стремиться к бесконечности, а аргумент W (р) при прохождении этих частот должен претерпевать приращение -180°, т. е. разрывы а. ф. х. должны дополняться полуокружностью бесконечного радиуса в направлении по часовой стрелке.

Это изображено на рис. 6.22. На рис. 6.22, а показана а. ф. х. разомкнутой системы, устойчивой в замкнутом состоянии. А. ф. х. построена только для положительных частот. При частоте и Р а. ф. х. уходит в бесконечность, асимптотически приближаясь к прямой, составляющей с осью вещественных угол, равный arg Wo (/Р).

Далее а. ф. х. дополнена полуокружностью бесконечного радиуса, и при со > р она возвращается из бесконечности вдоль той же асимптоты. Дальнейший ход а. ф. X. является обычным.

Из рис. 6.22, а видно, что а. ф. х. разомкнутой системы не охватывает точку (-1,70). В данном случае это должно соответствовать устойчивой замкнутой системе.

На рис. 6.22, б изображен другой случай, когда расположение а. ф. х. таково, что в замкнутом состоянии система оказывается неустойчивой, так как а. ф. X. охватывает точку (-1, /0).

Достоинством критерия Найквиста является возможность использования для определения устойчивости снятых экспериментально частотных характеристик. Это оказывается особенно ценнътм в том случае, когда ввиду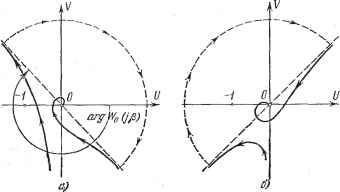

Рис. 6.22.

сложности исследуемой системы трудно получить исходные дифференциальные уравнения всей системы или ее отдельных блоков.

Большое практическое преимущество критерия Найквиста заключается также в том, что он может применяться при использовании логарифмических частотных характеристик, которые во многих случаях могут строиться почти без вычислительной работы. Этот вопрос будет рассмотрен в следующем параграфе.

В качестве иллюстрирующего примера рассмотрим следящую систему, избраженную на рис. 6.4. Для этой системы была получена передаточная функция разомкнутой системы

Нетрудно видеть, что все корни знаменателя, кроме одного нулевого корня, лежат в левой нблуплоскости. Поэтому в устойчивой системе амплитудно-фазовая характеристика не должна охватывать точку (-1, /0).

Частотная передаточная функция

W (ja)

Модуль ее

/(в(1-Ь/(в7у)(1-Ь/(вГм)-

и фаза

г1з (со) = - 90° - arctg соГу-arctg соГ = - 90° - arctg у

у-* м

Задаваясь различными значениями частоты от О до -j-oo, можно вычислить модуль и фазу. По модулю и фазе легко строится вектор W (/со) либо вычисляются предварительно вещественная и мнимая части частотной передаточной функции

и (со) = А (со) cos я]) (со), V {(о) = А (со) sin ip (со).

Ввиду достаточно простого выражения для частотной передаточной функции в данном примере можно легко найти U (со) и V (со), разлагая непосредственно комплекс W (/со) на вещественную и мнимую части:

)- (1 + сй2г) (1 + шГ) - ш (1 -Ь шГр (1 -Ь шГ)

Результаты расчетов сводятся в табл. 6.2.

Таблица 6.2

Примерный вид амплитудно-фазовой характеристики в случае устойчивой замкнутой системы изображен на рис. 6.23. Поскольку исходная передаточная функция имеет простой вид, задача получения устойчивости в расОматриваемой системе может быть решена в общем виде. Из рис. 6.23 следует, что для получения устойчивости точка пересечения амплитудно-фазовой характеристики с осью вещественных (точка а) должна лежать правее точки (-1, /0). Это условие можно записать следующим образом:

А (сй ) < 1.

Найдем частоту в точке а. Это можно сделать, взяв ОДНО из условий F (со) = О или ф (со) = - 180°, откуда получаем

Подстановка этой частоты

в записанное К

Рис. 6.23.

выше неравенство дает

или, после преобразования.

<1

Таким образом, получено условие, совпадающее с найденным ранее условием, вытекающим из критериев Гурвица и Михайлова.