где i? оо, a аргумент (-ф) меняется в пределах от + до--=-

На рис. 6.16, б изображен случай так называемой условно устойчивей системы. Здесь система будет устойчивой при значении общего коэффициента усиления, лежащем в некоторых пределах. Как увеличение, так и уменьшение общего коэффициента усиления К может привести к охвату годографом точки (-1, /0), что будет соответствовать неустойчивости системы в замкнутом состоянии.

На рис. 6.16, в изображен случай, когда система находится на границе устойчивости. Граница устойчивости будет колебательного типа. Это вытекает из того, что при некоторой частоте, при которой годограф пересекает точку (-1, /0), имеет место равенство W (/со) = - 1 + /О, что может быть записано в виде

1 + W (/со) = 0.

Последнее выражение представляет собой характеристическое уравнение, которое обращается в нуль при подстановке р = /со. Таким образом, чисто мнимый корень является решением характеристического уравнения.

На рис. 6.16, г изображен случай неустойчивой системы

Обратимся теперь к передаточной функции разомкнутой системы, соответствующей астатизму первого порядка. В этом случае передаточная функция может быть изображена в виде

тл / К (1 + Дт-1Р+..-+ДоР ) W- p(l-fC 2P-b...-fCoP -i)

Будем предполагать, что все корни знаменателя передаточной функции (кроме нулевого корня р = .0) Рис. 6.17. лежат в левой полуплоскости, т. е. в разомкнутом состоянии система является нейтрально устойчивой. Амплитудно-фазовая характеристика разомкнутой системы будет иметь разрыв непрерывности в точке со = 0. В этой точке модуль А (0) оо, а фаза делает скачок на 180°. Для получения определенности в ходе амплитудно-фазовой характеристики необходимо отнести нулевой корень знаменателя передаточной функции W (р) либо к левой, либо к правой полуплоскости корней (рис. 6.3). Первое является более удобным, так как при этом все корни знаменателя W (р) будут расположены в левой полуплоскости.

Для выполнения сказанного поступают следующим образом. При изменении частоты от - оо до -f оо происходит движение на плоскости корней вдоль оси мнимых снизу вверх (рис. 6.17). В начале координат расположен нулевой корень. Обойдем этот корень по полуокружности бесконечно малого радиуса так, чтобы корень остался слева. При движении по этой полуокружности против часовой стрелки независимая переменная р меняется по закону

р = pew,

где р О представляет собой радиус полуокружности, а ф - аргумент, меняющийся от -2 передаточная функция W[p) может

быть представлена в виде

Таким образом, во время движения по полуокружности бесконечно малого радиуса передаточная функция может быть представлена в виде вектора бесконечно большой длины, поворачивающегося на комплексной

плоскости по часовой стрелке на угол, равный л от до-- J, что соответствует полуокружности бесконечно большого радиуса.

На рис. 6.18 изображена амплитудно-фазовая характеристика абсолютно устойчивой системы с астатизмом первого порядка. Характеристика начинается в начале координат при со -оо и затем уходит в бесконечность при со О (верхняя ветвь). Далее характеристика дополняется полуокружностью бесконечно большого радиуса так, чтобы вектор W (/со) повернулся по часовой стрелке на угол л. Нижняя ветвь характеристики соответствует изменению частоты от О до Ч-оо.

Нетрудно видеть, что характеристика не охватывает точку (-1, /0), и система в замкнутом состоянии будет устойчивой.

Амплитудно-фазовые характеристики для условно устойчивой системы, для случая колебательной границы устойчивости и случая неустойчивой

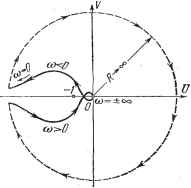Рис. 6.18.

Рис. 6.19.

системы будут похожими на изображенные на рис. 6.16, б, в ж г кривые, за тем исключением, что при со О характеристика будет уходить в бесконечность в соответствии с нижней ветвью характеристики, изображенной на рис. 6.18.

Аналогичными рассуждениями можно показать, что для системы с астатизмом второго порядка, имеющей передаточную функцию вида

. /fe(l+-Bm-lP+...+0P )

KV) - р2 (1 + с зР+ ... -Ь СоР -2)

при обходе двойного нулевого корня в начале координат (см. рис. 6.17) передаточная функция разомкнутой системы может быть представлена вектором бесконечно большой длины, поворачивающимся по часовой стрелке на угол 2к.

На рис. 6.19 изображена амплитудно-фазовая характеристика абсолютно устойчивой системы при наличии астатизма второго порядка. Так же как и ранее, здесь можно получить условную устойчивость (рис. 6.19), колебательную границу устойчивости, если характеристика пройдет через точку (-1, /0), и неустойчивость, если характеристика будет охватывать точку (-1, /0).

Обобщая проведенные рассуждения, получаем, что для определения устойчивости системы с астатизмом любого порядка достаточно построить только одну ветвь амплитудно-фазовой характеристики, соответствующую положительным частотам, которая должна быть дополнена окружностью бесконечно большого радиуса. При этом для устойчивой в замкнутом состоянии системы эта ветвь вместе с частью окружности, заключенной меноду

положительной полуосью вещественных и амплитудно-фазовой характеристикой, соответствующей положительным частотам, не должна охватывать точку (-1, /0) в соответствии с рис. 6.20.

Из рис. 6.20 следует, что абсолютная устойчивость может быть получена при степени астатизма г<2. При большей степени астатизма может быть получена только условная устойчивость.

Обратимся теперь к более общему случаю, когда знаменатель передаточной функц1ш разомкнутой системы с любой степенью астатизма содержит корни, лежащие в правой полуплоскости. Это соответствует неустойчхшой в разомкнутом состоянии системе.

Появление неустойчивости разомкнутот ! системы может вызьшаться двумя причинами. Во-первых, это может быть следствием наличия неустойчивых звеньев, подобных рассмотренным в § 4.8. Во-вторых, это может быть следствием потери устойчивости звеньев, охваченных положительными или отрицательными обратными связями (см., например, рис. 5.5).

Наличие неустойчивости системы в разомкнутом состоянии не означает, что система будет неустойчивой в замкнутом состоянии. Она может быть как устойчивой, так и неустойчивой. Однако формулировка критерия устойчивости Найквиста при этом несколько меняется. Пусть знаменатель передаточной функции разомкнутой системы (6.28) содержит I корней в правой полуплоскости и п - Z корней - в левой. Тогда при изменении частоты от -оо до +00 для устойчивой в замкнутом состоянии системы результирующий угол поворота годографа вектора W (/со) относительно точки (-1, /0) должен составить

113 = 4131 - г1з2 = пл - [{п - Z) л - Ы] = 1-2п,

т. е. амплитудно-фазовая характеристика должна охватить точку (-1, /0) столько раз, сколько корней в правой полуплоскости содержит знаменатель передаточной функции разомкнутой системы. При этом необходимо, чтобы