чается при = О, что дает условие Гу = 0. Это условие выполняется на оси абсцисс.

Таким образом, область устойчивости в плоскости параметров К ж Ту получена окончательно. Для любых значений К м Ту можно сразу ответить, устойчива или неустойчива система, смотря по тому, попадает или не попадает точка, определяемая этими значениями параметров, в область устойчивости.

§ 6;5. Критерий устойчивости Найквиста

В главе 5 было введено понятие передаточной функции разомкнутой системы. Эта функция может быть представлена в виде

Q (р) cop -fcip -l-f ... -fc

(6.28)

причем степень числителя не может быть выше степени знаменателя, тп. При подстановке р - /со получается частотная передаточная функция разомкнутой системы

= IS = с/ (со) + jV (со).

(6.29)

Частотная передаточная функция разомкнутой системы представляет собой комплексное число. На основании рассмотренных в главе 4 частотных характеристик смысл ее можно объяс-

нить следующим образом (рис. 6.13). Представим себе систему регулирования в разомкнутом состоянии в виде некоторого звена с передаточной функцией W (р). Если на вход этого звена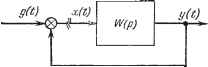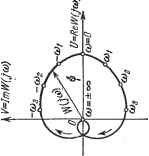

Рис. 6.13.

Рис. 6.14.

подавать сигнал ошибки в виде гармонических колебаний х = Хщах sin со с амплитудой Хщах и частотой со, то в установившемся режиме на выходе регулируемая величина будет изменяться также по гармоническому закону у= Ушах sin (cot + с амплитудой Утах> той же частотой со и фазовым сдвигом г1з. Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин:

л max

а аргумент - сдвиг фаз

Если изменять частоту входного воздействия от -оо до -Ьоо и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудт но-фазовую характеристику разомкнутой системы (рис. 6.14).

Ветвь этой характеристики, соответствующая отрицательным частотам, является зеркальным отражением ветви, соответствующей положительным частотам, относительно вещественной оси.

На амплитудно-фазовой характеристике для удобства могут отмечаться точки, соответствующие определенным частотам, например coj, а, cog и т. д. Вдоль кривой иногда рисуют стрелки, которые показывают направление возрастания частоты со (рис. 6.14).

В реальных системах всегда удовлетворяется условие m < п. Поэтому при частоте, стремящейся к бесконечности, модуль частотной передаточной функции стремится к нулю и точка с частотой со ± оо попадает в начало координат.

Сформулируем достаточные и необходимые требования к амплитудно-фазовой характеристике разомкнутой системы, при выполнении которых система автоматического регулирования в замкнутом состоянии будет устойчивой.

Ограничим вначале задачу и будем рассматривать только такие передаточные функции (6.28), которые соответствуют статическим системам. Это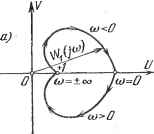

Рис. 6.15.

значит, что знаменатель (6.28) не будет иметь в качестве множителя оператор j3. Кроме того, будем пока рассматривать только устойчивые в разомкнутом состоянии системы. Это значит, что полюсы выражения (6.28), т. е. корни уравнения

СоР + Cip -1 + . + Cn-iJ3 + с = О,

лежат в левой полуплоскости.

Введем в рассмотрение вспомогательную функцию

где числитель

D (р) = Goja -f Gip -i + .. + n-lJ3 +

представляет собой характеристический полином системы. Сделаем подстановку р = /со и найдем комплекс

Q (/а)

(6.30)

(6.31).

(6.32)

(6.33)

Будем теперь изменять частоту от -оо до -)-оо и изобразим псчучив-шуюся амплитудно-фазовую характеристику (/со) на комплексной плоскости (рис. 6.15, а). Рассмотрим результирующий угол поворота вектора Wi (/со) при изменении частоты от - оо до -)-оо. Этот угол представляет собой изменение аргумента (6.33), который по правилу деления комплексных чисел равен разности аргументов числителя и знаменателя 2-

Ф = iJJl - 1132.

Числитель (6.33) представляет собой характеристический комплекс. Если все корни характеристического уравнения лежат в левой полуплоскости,

то при изменении частоты от -оо до -j-сю аргумент D (/со) изменится на величину ijjj = пп, где п - степень характеристического полинома. При построении кривой Михайлова результирующий угол поворота был равен

я!?, = п, но там частота изменялась от О до .--оо.

Знаменатель (6.33) представляет собой комплекс той же степени п, причем по предположению все корни (6.30) лежат в левой полуплоскости.

Рис. 6.16.

Поэтому результирующий угол поворота вектора Q (/со) при изменении частоты от -оо до -foo будет равен ilg = пп.

Отсюда следует, что в рассматриваемом случае результирующий угол поворота вектора W- (ja)) будет равен нулю: -ф = -ф - тф = 0. Это означает, что для устойчивой в замкнутом состоянии системы годограф вектора Wi Цо) не должен охватывать начала координат (рис. 6.15, а).

Частотная передаточная функция W (/со) отличается от вспомогательной функции Wi (/со) на единицу. Поэтому можно строить амплитудно-фазовую характеристику разомкнутой системы по выражению (6.29), что проще. Но в этом случае амплитудно-фазовая характеристика не должна охватывать точку с координатмми (-1, /0). Это является достаточным и необходимым условием того, чтобы система была устойчивой в замкнутом состоянии (рис. 6.15, б).

При определении устойчивости достаточно построить амплитудно-фазовую характеристику только для положительных частот, так как ее ветвь, соответствующая отрицательным частотам, может быть легко получена зеркальным отображением относительно оси вещественных.

На рис. 6.16, а изображен случай так называемой абсолютно устойчивой системы. Этот термин означает, что система остается устойчивой при любом уменьшении .коэффициента усиления разомкнутой цепи. Напомним, что передаточная функция. разомкнутой статической системы может быть представлена в виде

Нетрудно видеть, что уменьшение общего коэффициента усиления К приводит к уменьшению модуля (6.29), а это в случае, изображенном на рис. 6.16, а, не может привести к охвату годографом точки (-1, /0).