urk,B

>

Как видно, уже для уравнения пятой степени условия устойчивости по критерию Гурвица получаются достаточно громоздкими. Поэтому использование этого критерия практически ограничивается уравнениями четвертого порядка.

Существенным недостатком критерия Гурвица является также то, что для уравнений высоких порядков в лучшем случае можно получить ответ

о том, устойчива или неустойчива система автоматического регулирования. При этом в случае неустойчивой системы критерий не дает ответа на то, каким образом надо изменить параметры системы, чтобы сделать ее устойчивой. Это обстоятельство привело к поискам других критериев, которые были бы более удобными в инженерной практике.

Для иллюстрации применения критерия Гурвица рассмотрим пример на определение устойчивости дистанционной следящей системы. Принципиальная и структурная схемы изображены на рис. 6.4. В качестве чувствительного элемента использованы два сельсина (СД и СП), включенные по трансформаторной схеме. Передаточная функция сельсинов равна коэффициенту передачи схемы:

Рис. 6.4.

где & = &! - ва - ошибка, равная разности углов поворота командной и исполнительной осей.

Передаточная функция усилителя:

где 2 - коэффициент усиления и Ту - постоянная времени усилителя. Передаточная функция двигателя (Д):

где кз

в. сек

-коэффициент передачи двигателя по скорости, а Т--элект-

ромеханическая постоянная времени двигателя совместно с оконечным каскадом усилителя.

Передаточная функция редуктора (Р) равна его коэффициенту передачи, определяемому передаточным отношением:

W,{p) = h.

Так как цепь регулирования состоит из включенных последовательно звеньев, то передаточная функция разомкнутой цепи будет равна произведению передаточ1п.1Х функций отдельных звеньев:

W ip) = W, ip) (р) Шз ip) W, ip) = ,,J,,,.

где K = kik2kJCi

общий коэффициент усиления разомкнутой цепи.

Характеристическое уравнение:

i-\-W{p)=0. После подстановки W (р) получаем

ТуТр + {Ту + Т)р + р + к = о.

Б данном случае характеристическое уравнение имеет третий порядок. Нетрудно видеть, что условие положительности всех коэффициентов выполняется всегда, если выполнено условие Kl>0, что будет при правильном согласовании направления вращения двигателя со знаком рассогласов ания.

Дополнительное условие а-ааа, накладываемое на коэффициенты характеристического уравнения, сводится при подстановке значений коэффициентов ( о = ГуГм, % = Ту -\- Гм, 2 = 1 и 3 = .ЙГ), к неравенству

которое и является условием устойчивости рассматриваемой системы.

Из этого неравенства, в частности, можно заметить, что увеличение каждой постоянной времени сказывается отрицательно на устойчивости системы, так как при этом снижается предельное значение общего коэффициента усиления К, при котором система еще остается устойчивой.

§ 6.3. Критерий устойчивости Михайлова

Рассмотрим отдельно левую часть характеристического уравнения (6.9), которая представляет собой характеристический полином:

D {р) = аоТэ + iJ5 - 4- . . . + + п. (6.16)

Подставим в этот полином чисто мнимое значение jd = /cu, где со представляет собой угловую частоту колебаний, соответствующих чисто мнимому корню характеристического уравнения. При этом получим характеристический комплекс

D (/со) = Z (со) 4- jY (со) = D (со) (6.17)

где вещественная часть будет содержать четные степени со:

X (со) = о - а 2Со2 4- . . . . (6.18)

а мнимая - нечетные степени со:

У (со) = a iCO а зСО + . (6.19)

Функции D (со) и яр (со) представляют собой модуль и фазу (аргумент) характеристического комплекса.

Характеристический полином (6.16) не будет иметь корней е правой полуплоскости, если полное приращение фазы или аргумента ф (со) при изменении со от О до оо равно п , где п - степень полинома D {р). Следовательно, система регулирования будет устойчивой. Если полное приращение аргумента ij? (со) окажется меньше п у , то система неустойчива. Докажем это.

Если все коэффициенты заданы и задано определенное значение частоты со, то величина D (/со) изобразится на комплексной плоскости в виде точки с координатами Z и У или в виде вектора, соединяющего эту точку с началом координат. Если же значение частоты со менять непрерывно от нуля до бесконечности, то вектор будет изменяться по величине и по направлению, описывая своим концом некоторую кривую (годограф), которая называется кривой Михайлова (рис. 6.5).

КРИТЕРИИ устойчивости

[гл. 6

Практически кривая Михайлова строится по точкам, причем задаются различные значения частоты со и по формулам (6.18) и (6.19) вычисляются X (со) и Y (со). Результаты расчетов сводятся в таблицу, по которой и строится затем кривая.

Выясним связь между видом кривой Михайлова и знаками веществен-1П.1Х корней, характеристического уравнения. Для этого определим, чему должен равняться угол поворота if вектора D (ja) при изменении со от нуля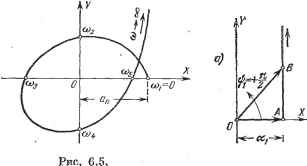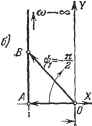

Рис. 6.6.

до бесконечности. Для этого запишем характеристический полином в виде произведения сомножителей

D (р) = ао [р - pi) {р - Pi) . . . {р ~ Рп), (6.20)

где Pi, . . ., Рп - корни характеристического уравнения.

Характеристический вектор можно тогда представить в следующем виде:

D и а) = о (; - Pi) (/со - р г) ... (/со - Рп).

(6.21)

Каждая из скобок представляет собой комплексное число. Следовательно, D (/со) представляет собой произведение п комплексных чисел. При перемножении аргументы комплексных чисел складываются. Поэтому результирующий угол поворота вектора D (/со) при изменении со от нуля до бесконечности будет равен сумме углов поворота отдельных сомножителей (6.21):

If = ifi + ifa +

+ Ifn.

(6.22)

Определим каждое слагаемое (6.22) в отдельности.

1. Пусть какой-либо корень, например р, является вещественным и отрицательным, т. е. Pi = - ttj, где tti Сомножитель в выражении (6.21), определяемый этим корнем, будет тогда иметь вид (а + /со).

Построим годограф этого вектора на комплексной плоскости при изменении со от нуля до бесконечности (рис. 6.6, а). При со = О вещественная часть X = ац а мнимая Y = 0. Этому соответствует точка А, лежащая на оси вещественных. При афО вектор будет изменяться так, что его вещественная часть будет по-прежнему равна а, а мнимая часть У = со (точка В на графике). При увеличении частоты до бесконечности конец вектора уходит в бесконечность, причем конец вектора все время остается на вертикальной прямой, проходящей через точку А, а вектор поворачивается против часовой

стрелки. Результирующий угол поворота вектора ifi = + -у

2. Пусть теперь корень р является вещественным и положительным, т. е. = + а, причем > 0. Тогда сомножитель в (6.12), определяемый этим корнем, будет иметь вид (-+ /со). Аналогичные построетя (рис. 6.6, б) показывают, что результирующий угол поворота будет ifi =