ГЛАВА 6

КРИТЕРИИ. УСТОЙЧИВОСТИ

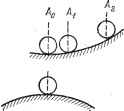А

Рис. 6.1.

§ 6.1. Понятие об устойчивости систем регулирования

Понятие устойчшости системы регулирования связано со способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Наглядно устойчивость равновесия иллюстрируется рис. 6.1, а, на котором изображен шар, лежащий в некотором углублении. При всяком отклонении его от положения равновесия он будет стремиться возвратиться к нему точно (при отсутствии сил трения) или к некоторой конечной области, окружающей предшествующее положение равновесия (при наличии сил трения). Такое положение шара будет устойчивьш.

На рис. 6.1, б изображен другой случай, когда положение шара оказывается неустойчивым. Рис. 6.1, в соответствует случаю безразличного положения равновесия.

Можно ввести понятия о невозмущенном состоянии равновесия, соответствующем точке Л о на рис. 6.1, а, и возмущенном состоянии равновесия (точка А. После прекращения действия внешних сил шар возвратится в точку А о или Условие устойчивости здесь можно сформулировать так: система называется

устойчивой, если из возмущенного состояния равновесия она перейдет в некоторую конечную область, окружающую не возмущенное состояние равновесия.

Понятие устойчивости можно распространить и на случай движения некоторой системы. Пусть ее состояние определяется независимьши координатами {t), x(t), . . ., Xj {t). Заданное движение системы определяется некоторым законом изменения координат: {t), Х20 (t), . . ., Хпо (t).

Аналогично случаю равновесия положения заданное движение можно назвать невозмущенным движением. Приложение внешних сил к рассматри-авемой системе вызовет отклонение действительного движения от заданного:

х {t) ф хю (О, (t) Ф 20 (t) и т. д.

Это движение будет возмущенным.

Заданное невозмущенное движение будет устойчивьш, если в результате приложения внешних сил, которые затем снимаются, возмущенное движение по истечении некоторого времени войдет в заданную область:

I Щ (t) - Xio (t) I < Ei (i = 1, 2, . . n).

Рассмотрим вопрос устойчивости более подробно. Пусть система регулирования описывается нелинейными дифференциальными уравнениями

в форме Коши

= Fi{x ... хп) (i = 1, 2, ..., п). : (6.1)

Если при t = tc, заданы начальные значения (i = i, 2, . . ., п), то решение может быть представлено в виде xi = xt (х-ю, хц), где i = 1, 2, . . ?г.

Пусть установившиеся процессы в системе характеризуются координатами ж, ж , .... х. Введем также отклонения координат Axf = xi - х\ (i = 1, . . ., ?г), характеризующие отклонения процесса от установившегося.

Систему уравнении (6.1) перепишем для отклонении:

= /, (Аж Ах Аж ), (6.2)

где fi - некоторые нелинейные функции. Эти уравнения называются уравнениями возмущенного движения. Их тривиальные решения Дж? = О соответствуют невозмущенному движению, так как при этом xt = ж?.

Начальные значения отклонений Джо носят название возмущений. Решение системы (6.2) для некоторых начальных отклонений Дж = = Axi (Ахщ, . . Ажпо. t) представляет собой возмущенное движение.

А. М. Ляпунов [821 дал следующее определение устойчивости.

Невозмущенное движение (при Ах\ = 0) называется устойчивым по отношению к переменным Xt, если при всяком заданном положительном числе А, как бы мало оно ни было, можно выбрать другое положительное число [А так, чпю для всех возмущений Axto, удовлетворяющих условию

2 iДж? <x (6.3)

возмущенное движение (6.2) будет для времени tT удовлетворять неравенству

SгfДжf<4 ; (6.4)

Здесь рг - некоторые весовые коэффициенты, необходимые для уравнивания физических размерностей величин Дж.

Геометрическая интерпретация этого условия заключается в следующем. В пространстве координат РгДжг построим две сферы с радиусами К в. А. Система будет устойчивой, если при возмущениях, не выведших изображающую точку М (Джю, . . ., Джпо) из пределов сферы X, возмущенное движение будет таково, что, начиная с некоторого времени tT, изображающая точка М (Axi, . . ., Дж ) будет в пределах сферы А.

Если с течением времени изображающая точка стремится к началу координат, т. е.

ЦшДжг = 0 (i = l, 2, ;г),

то система асимптотически устойчива.

Несколько другое изложение этой теоремы будет дано ниже в § 16.1.

Перейдем теперь к вопросу устойчивости линейных, а точнее, линеаризованных систем регулирования.

Рассмотрим дифференциальное уравнение движения линеаризованной системы автоматического регулирования, записанное для регулируемой величины у (t) при наличии задающего воздействия g (t) и при равенстве нулю

возмущающих воздействий:

(аоР + aiP - + ... + а + an) у (t) =

= (ЬоР + М - + . . . + Ьгг-гР + Ъ) g (t). (6.5)

Коэффициенты 5 . . .-, а-шЪ, . . представляют собой постоянные

величины, а оператор р = -чг-

Дифференциальное уравнение движения системы регулирования можно записать и для возмущающего воздействия. В этом случае левая часть (6.5) останется без изменения, а правая часть будет иметь иной вид. В общем виде дифференциальное уравнение, определяющее изменение регулируемой величины, может быть записано так, что в лравой его части будет находиться некоторая функция времени / (t).

Характер переходных процессов в системе определяется видом левой части дифференциального уравнения (6.5). Поэтому для определения качественной картины переходных процессов является практически безразличным, записать ли исходное дифференциальное уравнение для управляющего или возмущающего воздействия.

Уравнение (6.5) может с равным успехом быть записано для ошибки регулирования X (t). При этом левая часть уравнения (6.5) полностью сохраняет свой вид.

Процесс регулирования определяется решением дифференциального уравнения как сумма двух решений - частного решения неоднородного уравнения (6.5) с правой частью и общего решения уравнения (6.5) без правой части, т. е. с правой частью, равной нулю:

v(t) частн it) + Уобщ it) (6.6)

Bj случае Удастн (*) = const это будет установившееся значение. Первое слагаемое (6.6) называют также вынужденным решением у (t), а второе слагаемое - переходной] составляющей у (t). Тогда формула (6.6) может быть записана в виде

У (t) = Уэ U) + Уп (t).

Система будет называться устойчивой, если с течением времени при t- оо переходная составляющая будет стремиться к нулю: у (t) 0. Найдем эту составляющую из (6.5). Для этой цели необходимо решить дифференциальное уравнение без правой части

Общее решение ищется в виде

Уи (t) = Уобщ (t) = Себ .

Дифференцируя это выражение п раз и подставляя в (6.7), получаем после сокращения на общий множитель Се*

аЛ -f %S -i -f. . . + a iS + On = 0. (6.8)

Полученное алгебраическое уравнение называется характ,еристическим. Корни его Sj, . . ., Sn будут определять характер переходного процесса в системе. Нетрудно заметить, что по своему виду левая часть (6.8) полностью совпадает с левой частью (6.5). Поэтому характеристическое уравнение получается приравниванием левой части (6.5) нулю:

а,р + аио -1 -Ь . . . + Ч- й = 0. (6.9)