§ 5.7. Уравнения следящей системы

Рассмотрим следящую систему, иринциииальная схема которой изображена на рис. 5.18. Задающим устройством является командная ось КО, вращаемая извне по произвольному закону &! = {t). Этот угол должен повторяться на управляемом объекте УО, ось которого является исполнительной осью ИО. Мощность, требуемая для вращения командной оси, ничтожна, так как с командной осью сцеплен только движок потенциометра П. Мощность, которую может потреблять для своего вращения управляемый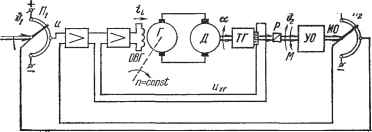

Рис. 5.18.

объект, значительно выше и обеспечивается установкой двигателя Д соот-. ветствующей номинальной мощности. В этом, а также в дистанционности управления заключается смысл использования подобной следящей системы воспроизведения угла поворота.

Сравнение углов поворота командной и исполнительной осей осуществляется при помощи двух потенциометров и iZj. Если углы поворота командной и исполнительной осей не равны, &] Ф Ь, то возникает напряжение рассогласования и, которое поступает на вход первого электронного-усилителя. Далее усиленный сигнал после прохождения через два электронных усилителя подводится к обмотке возбуждения генератора ОВГ, привод которого не показан на схеме. Якорь генератора Г соединен с якорем двигателя Д, обмотка которого {ОВД) подключена к постоянному напряжению.. В результате при появлении рассогласования & = &! - &2 двигатель начинает вращаться в сторону уменьшения ошибки до согласования двух осей. Задающим воздействием здесь является угол поворота &! {t). В качестве-возмущающего воздействия рассмотрим момент нагрузки М {t) на оси управ-, ляемого объекта.

Для улучшения динамических качеств следящей системы в ней предусмотрена отрицательная обратная связь по напряжению тахогенерато-ра (ГЛ.

Будем считать, что все звенья системы линейны, за исключением электро-мапшнного усилителя (генератора), у которого электродвижущая сила & связана с током возбуждения нелинейной кривой намагничивания генератора. Однако и здесь при сравнительно небольших напряжениях якоря (примерно до половины номинального) можно зависимость между е и 1д считать также линейной.

Таким образом, в рассматриваемой системе отпадает необходимость линеаризации и можно сразу приступить к составлению уравнений. Для этой цели разобьем систему на динамические звенья и найдем их передаточные функции.

Чувствительный элемент. Напряжение на выходе первого потенциометра будет щ = /ci&i и на выходе второго = кЬ, где

рад

- крутизна

или коэффициент передачи потенциометра. Напряжение на выходе чувствительного элемента равно разности

u = Ui~U2 = ki (&! - йг) = kj. (5.101)

Это дает передаточную функцию, чувствительного элемента

W, (р) = h. (5.102)

Электронные усилители. Считая усилители безьшерционными, молено записать их передаточные функции в виде

(р) = к, (5.103)

Ws {р) = ks, (5.104)

где h ж кз коэффициенты усиления но напряжению первого и второго усилителей.

Обмотка возбуждения генератора. Дифференциальное уравнение можно записать на основе второго закона Кирхгофа:

/-в- + Гв1в = Мвых, (5.105)

где Гв и Lj, - суммарные сопротивление и индуктивность цени возбуждения с учетом выходного каскада усилителя.

Приведем это уравнение к стандартному виду:

{T,p + l)i. = =k,u,, (5.106)

где Гв = - - постоянная времени цени возбуждения.

Отсюда находим передаточную функцию обмотки возбуждения:

Генератор. Для прямолинейной части характеристики намагничивания можно положить

е = ki, (5.108)

где h - коэффициент пропорциональности между э. д. с. генератора и током возбуждения в линейной части характеристики. Отсюда получаем передаточную функцию генератора:

Wip) = h. (5.109)

Двигатель. Так как при фиксированном возбуждении двигатель имеет две степени свободы, то необходимо иметь для него два исходных дифференциальных уравнения. Первое уравнение может быть получено, если записать второй закон Кирхгофа для цени якоря:

/я + гА + СвФОе. (5.110)

Второе уравнение представляет собой закон равновесия моментов на валу двигателя:

СкФя~М (5.111)

В этих уравнениях Z/я и - индуктивность и сопротивление цепи якоря (суммарные). Се и См - коэффициенты пропорциональности, / - приведенный к оси двигателя суммарный момент инерции, £2 - угловая скорость двигателя, Ф - поток возбуждения, М - момент нагрузки, приведенный к валу двигателя.

СЬФ = С =

СмФ = С=

где [/ном и /я.ном - номинальные значения напряжения и якорного тока двигателя, Мном и Qx - номинальный вращающий момент и скорость идеального холостого хода двигателя.

Учитывая эти соотношения, электромеханическую постоянную времени можно представить в другом виде:

йхх -

ном Л/ном М-

где Гном = - номинальное сопротивление якоря двигателя, Мкз -

я-ном

момент короткого замыкания двигателя (вращающий момент заторможенного двигателя).

В формуле (5.155) перейдем к углу поворота двигателя а, который связан с угловой скоростью Q зависимостью Q = ра:

{ТТр + Тир + 1)ра---+J,f . (5.116)

Из последн(-го выражения, сравнивая его с формулой (5.9), можно получить передаточную функцию двигателя, связывающую его угол поворота а с э. д. с. генератора:

и передаточную функцию по возмущению, связьшающую угол поворота а с моментом М, приложенньш к его оси:

Редуктор. Считая редуктор линейным безынерционным звеном, запишем его передаточную функцию в виде

W7(p) = -f, (5.119)

где i > 1 - передаточное отношение редуктора.

Так как поток возбуждения двигателя Ф = const, то можно положить СеФ = Се ш СмФ = См-

Вводя оператор дифференцирования и решая уравнения (5.110) и (5.111) совместно, получаем

(ГяГмР + ТиР +1) £2 = --liliI. (5.112)

Здесь введены две постоянные времени двигателяГэлектромеханическая постоянная времени

г. = (5-113)

и постоянная времени якорной цепи

?я = . (5.114)

Коэффициенты пропорциональности С и Сд могут, быть найдены из соотношений