называется импульсным. Если последующее звено системы тоже дискретное, то для него не только выходная, но и входная величина будет дискретной (импульсной), к дискретньш автоматическим системам относятся системы

Рис. 1.10.

импульсного регулирования (т. е. системы с импульсным звеном), а также системы с, цифровыми вычислительными устройствами. Эти последние дают результат вычисления на выходе дискретно, через определенные промежутки

времени, в виде чисел для отдельных дискретных числовых значений входной величины.

Системой релейного действия называется такая система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина в некоторых точках процесса, зависящих от значения входной величины, изменяется скачком. Такое звено называется релейным звеном.

Рис. 1.11.

\ \ \ г Статическая характеристика релейного звена имеет точки разрыва, как показано в разных вариантах на рис. 1.12.

Обратимся теперь ко второму признаку классификации автоматических систем. Линейной системой называется такая система, динамика всех звеньев которой вполне описывается линейными уравнениями (алгебраическими я дифференциальными или разностными). Для этого необходимо прежде всего, чтобы статические характеристики всех звеньев системы были линейными, т. е. имели вид прямой линии (рис. 1.10, а и б).

§ 1.2]

КЛАССИФИКАДИЯ АВТОМАТИЧЕСКИХ СИСТЕМ

Если динамика всех звеньев системы описывается обыкновенными линейными дифференциальными (и линейными алгебраическими) уравнениями с постоянными коэффициентами, то систему называют обыкновенной линейной системой.

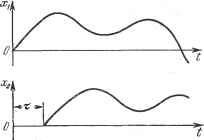Рис. 1.12.

Если в уравнении динамики какого-либо звена линейной системы имеется хотя бы один или несколько переменных во времени коэффициентов, то получается линейная система с переменными параметрами. Если какое-либо звено описывается линейным уравнением в частных производных (например, имеют место волновые процессы в трубопроводе или в электрической линии), то система будет линейной системой с распределенными параметрами. В отличие от этого обыкновенная линейная система является системой с сосредоточенными параметрами. Если динамика какого-либо звена системы описывается линейным уравнением с запаздывающим аргументом (т. е. звено обладает чисто временным запаздыванием или временной задержкой т передачи сигнала (рис. 1.13)), то система называется линейной системой

с запаздыванием. Динамика линейных импульсных систем описывается линейными разностными уравнениями. Все эти системы объединяются общим названием особые линейные системы, в отличие от обыкновенной линейной системы, указанной выше.

Заметим, что хотя классификация систем и производится по уравнениям динамики звеньев, в дальнейшем будет применяться исследование динамических процессов не только с помощью аппарата уравнений, но также и с помощью эквивалентного ему частотного аппарата, в большинстве случаев более удобного для практических приложений.

Нелинейной системой называется такая система, в которой хотя бы в одном звене нарушается линейность статической .характеристики или же имеет место любое другое нарушение линейности уравнений динамики звена (произведение переменных или их производных, корень, квадрат или более высокая степень переменной, любая другая нелинейная связь переменных и их производных).

Рис. 1.13.

Следовательно, к нелинейным системам относятся, в частности, все системы, в звеньях которых имеются статические характеристики любого-из многих видов, показанных на рис. 1.10, в-и. К ним же относятся и все системы релейного действия (рис. 1.12).

Нелинейными могут быть, разумеется, также и системы с переменными параметрами, с распределенными параметрами, с запаздыванием, импульсные и цифровые системы, если в

Особое линейное аВено

Обыкновенная линейная шсть

Нелинейное гбено

Линейная часть

Рис. 1.14.

них где-либо нарушается линейность уравнений динамики (в цифровых системах это связано, в частности, с квантованием сигнала по уровню). J При исследовании, расчете и синтезе автоматических систем нужно иметь в виду, что наиболее полно разработаны теория и различные прикладные методы для обыкновенных линейных систем.. Поэтому в интересах простоты расчета всегда желательно (там, где это допустимо) сводить задачу к такой форме, чтобы максимально использовать методы исследования обыкновенных линейных систем. Обычно уравнения динамики всех звеньев системы стараются привести к обыкновенным линейным, и только для некоторых звеньев, где это недопустимо или где специально вводится особое линейное или нелинейное звено, учитываются эти особые их свойства. Тогда при наличии одного такого звена система при расчете разбивается на два блока (рис. 1.14), в одном из которых объединяется весь комплекс обыкновенных линейных звеньев.

Однако это вовсе не значит, что при проектировании новых автоматических систем нужно стремиться к обыкновенным линейным системам. Наоборот, уже из приведенных выше определений совершенно очевидно, что обыкновенные линейные системы обладают ограниченными возможностями. Введение особых линейных и нелинейных звеньев может придать системе лучшие качества. Особенно богатыми возможностями обладают системы со специально вводимыми нелинейностями и дискретные системы, в том числе с цифровыми вычислительными устройствами, а также адаптивные, т. е. самонастраивающиеся, экстремальные, самоорганизующиеся систелш.

§ 1.3. Примеры непрерывных автоматических систем

Один из первых в истории техники автоматических регуляторов был изобретен И. И. Ползуновым в 1765 г. Это был автоматический регулятор уровня воды в котле его паровой машины (рис. 1.15). Здесь полностью осуществлен общий принцип действия любого автоматического регулятора прямого действия (рис. 1.7). Измерительное устройство (поплавок), измеряющее регулируемую величину (высоту уровня воды в котле), непосредственно перемещает регулирующий орган (клапан питания котла водой). Котел является регулируемым объектом.

Изменение величины отбора пара из котла в паровую машину является основным возмущающим воздействием на регулируемый объект. Если отбор пара увеличится, испарение воды ускорится, уровень воды Н (регулируемая величина) начнет уменыпаться. Тогда поплавок, опускаясь, будет шире открывать регулирующий клапан, усилится приток питающей воды, и уровень ее будет автоматически восстанавливаться. Кроме изменения отбора