например, если то = 3, А; = 2 и Z = О, то из (5.72) и (5.73) можно получить для изображений

у\ {р) = W4, (р) и, (р) + w?2 ip) {р),

Y, [р) = W°2i (р) и, [р) + W°22 (р) и, ip), Уз ip) = Hli ip) и, ip) + Wl ip) и, ip).

(5.75)

Если в матрице передаточных функций объекта (5.73) или (5.74) для каждого элемента матрицы (частной передаточной функции) найти обратное преобразование Лапласа (оригинал), то будет получена так называемая матрица Коши (матрица весовых функций). Запишем ее, например, для управляющих воздействий:

wu Ц) wiz it) ... it)

Wuit) Wiiit) Wihit)

Wo it) =

Wm\it) Wmsit) ... Wmkit)

(5.76)

Если в момент времени f = О на все входы поступают управляющие воздействия Ui it), где г = 1, 2, . . ., /с, то изменение j-ii регулируемой величины может быть записано посредством интеграла Дюамеля - Карсона (4.9) на основании принципа суперпозиции:

h t

У j it) I Ui it) Wjiit~x)dx.

i=i 0

Ha рис. 5.13 изображена условная структурная схема замкнутой многомерной системы регулирования. На схеме все указанные символы соответствуют матрицам: g it) - задающих воздействий, z/(f)~ регулируемых величин, a;(f)- ошибок для каждой регулируемой величины, и it) - управляющих воздействий, / it) - возмущений. Wo ip) - передаточных функций для управлений, W ip) - передаточных функций для возмущений. Кроме того, введена прямоугольная матрица передаточных функций регулирующего устройства Ирег ip) = 11 kji ip) Пьхтп которая определяет используемые законы регулирования. Она дает связь между изображениями управляющих величин и овзибок: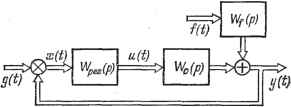

Рис. 5.13.

Uip) =

(5.77)

Уравнения многомерной системы (рис. 5.13) могут быть получены действиями, аналогичными одномерному случаю (§ 5.2).

Матрица передаточных функций разомкнутой но всем каналам системы

W ip) = Wo ip) РУрег ip).

(5.78)

Характеристическая матрица системы представляет собой квадратную матрщу размером т X т:

Z) (р) = / + W (р) = II dn (р) II (5.79)

Здесь / - единичная матрица размером т X т, i. е. квадратная матрица, у которой все элементы главной диагонали равны единице, а остальные - нулю.

Характеристическое уравнение системы получается приравниванием нулю определителя характеристической матрицы:

I Z) (р) 1 = I Л- ТУ (р) I = 0. (5.80)

Заметим, что в случае, когда многомерная система представляет сово-жупность т независимых одномерных систем, характеристическая матрица будет диагональной и определитель системы тогда равен произведению частных определителей каждой из систем, т. е. Z) (р) = (р) X ... ... X I (р) . В этом случае общее характеристическое уравнение распадается на т независимых характеристических уравнений Z)j (р) = О, i = 1, 2, . . ., т.

Матрицы передаточных функций замкнутой системы, замкнутой системы по ошибке и замкнутой системы по возмущениям при условии, что матрица D (р) неособая, что означает независимость исходных дифференциальных уравнений, могут быть определены из выражений

Ф (р) = (р) W (р) = -jlgb W ip),

ф.(р)=5-чр)=т,

Ф/ ip) = Dr iP) Wf (;>) = тт Wf ip).

(5.81) (5.82) (5.83)

Здесь D (p) = II Dji (p) llmxm - матрица, присоединенная для матрицы В (р), а Dji (р) - алгебраическое дополнение определителя D (р) .

Полученные выражения для матриц передаточных функций замкнутой системы позволяют использовать формулы, аналогичные формулам § 5.2, но записанные уже для матриц-столбцов ошибок и регулируемых величин. Так, например, для матрицы изображений опшбок имеем

1 (Р)

Х{р) =

хар)

Х (р)

==0.{P)G{p)~Of{p)F{p).

(5.84)

На рис. 5.14 изображены для иллюстрации некоторые структурные схемы двумерных систем регулирования. Схема на рис. 5.14, а соответствует так называемому сепаратному регулированию объекта с двумя входами и двумя выходами. Матрица передаточных функций регулирующего устройства в этом случае получается диагональной. Матрицу изображений управляющих величин для этого случая можно представить в виде

и lip) и Ар)

= ТУрег(р)Х(р) =

hi ip) О

о / 22 ip)

Xi ip)

хАр)

(5.85)

Схемы на рис. 5.14, бив соответствуют комбинированному регулированию. В этом случае

Исходные дифференциальные уравнения многомерной системы регулирования могут быть также представлены в форме Коши в матричной записи:

=Ax + Bu + Ef,

(5.87)

у = Сх, u = Dx.

В этих выражениях х = \\xi \\

матрица-столбец фазовых координат

системы, п - порядок дифференциального матрица-столбец регулируемых величин, = llixb - матрица-столбец управляющих величин, / = II /г Нхг - матрица-столбец возмущающих и задающих воздействий, = II fji Wnxn - квадратная матрица коэффициентов, 5 = II bji хь, С = II Cji llmxn, D = II dji II fexn и £ = II en II хг - прямоугольные матрицы коэффициентов.

Величины (j = 1, 2, . . ., тг) представляют собой некоторые абстрактные величины, задание которых полностью определяет текущее состояние системы. Эти величины называются фазовыми координатами системы. Состояние системы может быть также отождествлено с положением изображающей точки в тг-мерном пространстве, которое носит название пространства состояния.

При переходе к изображениям и совместном решении система уравнений может быть приведена, например, к виду (5.84),

уравнения, у = z/j jxro -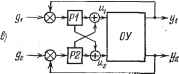

Рис. 5.14.

Характеристическое уравнение, соответствующее системе (5.87), имеет

\1р - А - BD \ =0, (5.88)

где / - единичная матрица п X п.

Векторная запись исходных уравнений. Введем в рассмотрение п-мер-ное векторное пространство состояния, которое определяется базисом (набором векторов) е = 11 ее ... e,i так, что с матрицей-столбцом фазовых координат а; = II хх . . . х \\ может быть отождествлен вектор состояния

X = еж-! 4- ех 4- . . + е-х. (5.89)

Длины векторов базиса (j = 1, . . ., тг) играют роль весовых коэффициентов в переходе от матрицы-столбца фазовых координат к вектору состояния. Заметим, что в общем случае, когда рассматриваются абсолютные, а не относительные значения фазовых координат, их физические размерности не совпадают и длины векторов базиса не могут считаться единичными.

Аналогичным образом может быть введено векторное пространство управления, возмущения и выходных величин.

При] введении векторов х, и, f ж у исходные уравнения системы могут быть записаны в векторной форме:

=Ax-Bu-Ef, у = Сх,

u = Dx.