доиолнительные передаточные функции, определяемые выражениями

Полученная в результате преобразования схема (рис. 5.9, е) уже относится к простейшим.

Использование графов. Подобно структурным схемам графы прохождения сигналов используются для наглядного изображения математических зависимостей в системах регулирования. Графом (рис. 5.10, б) называется множество вершин и ребер. Каждому ребру соответствуют две вершины - начало и конец ребра. Вершине и ребру могут быть сопоставлены или некоторые величины, НЛП операторы, например передаточные функции.

Основные свойства графов прохо?к-дения сигналов следующие.

а) У

X я, Xg W2 ж, Щ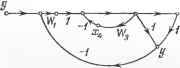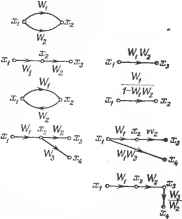

д:, ц

-ох, X, а

1 Щх,г

Рис. 5.10.

Рис. 5.11.

1. Каждая вершина, отмеченная на графе кружком или точкой, соответствует некоторой переменной (координате) рассматриваемой системы.

2. Каждое ребро графа, изображаемое в виде линии со стрелкой, указывающей направление прохождения сигнала, имеет вершпну-начало (входную величину) п вершину-конец (выходную величину). Еслп из вершиньт выходит несколько ребер, то все они имеют одинаковую входную величину.

3. Выходная величина ребра получается как результат преобразования, осуществляемого соответствующим рсбрз оператором, входной величины ребра.

4. Ес.т1и к одной вершине подходит несколько ребер, то величина, соответствующая этой вершине, получается а.!1гебраическ1ш суммированием выходных величин этих ребер.

Между структурной схелюй и графом прохождения сигналов имеется прямое соответствие: прямоугольник структурной схед1ы соответствует ребру, а лпния передачи cnrna.Tia - вершине графа.

На рис. 5.10 для сравнения изображены одновременно структурная схема (а) и граф прохождения сигналов (б) одной и топ же системы.

Правила преобразования графов подобны правилам преобразования структурных схем линейных систем. Эти правп.ча изображены на рис. 5.11 в виде исходных (первый столбец) и эквивалентных (второй столбец) схем.

В дальнейшем изложении будут использоваться более удобные структурные схемы.

§ 5.5]

МНОГОМЕРНЫЕ СИСТЕМЫ РЕГУЛИРОВАНИЯ

т). Это имеет место

г I I I I I,

-у>

§ 5.5, Многомерные системы регулирования

К многомерным относятся системы управления и регулирования, имеющие несколько регулируемых величин уг (i = 1, 2, . . во многих современных сложных системах. К ним относятся, например, системы регулирования напряжения и частоты синхронных генераторов, системы управления подвижных объектов, многие системы регулирования технологических процессов и др.

Многомерная система предполагает наличие многомерного объекта управления (рис. 5.12), который характеризуется существованием нескольких входов (точек приложения управляющих и возмущающих воздействий) и нескольких выходов, определяемых регулируе-мьши величинами.

Многомерный обтэокт описывается системой уравнений, которую удобно представлять в матричной форме.

Введем одностолбцовую т-мерную матрицу регулируемых величин

Рис. 5.12.

= 11 ут---Ут\\,

(5.64)

одностолбцовую /с-мерную матрицу управляющих величин

(5.65)

и одностолбцовую /-мерную матрицу возмущающих воздействий

= \\hU---fi\\-

(5.66)

Здесь штрихом обозначена операция транспонирования матригсы.

Если регулируемые величины имеют одинаковую физическую размерность и могут трактоваться как проекции некоторого вектора на оси координат, матрща-столбец может отонадествляться с вектором. Тогда можно говорить о векторе регулируемых величин.

Если регулируемые величины имеют разную физическую размерность, то переход от матрицы-столбца к вектору в принципе может быть сделан и в этом случае, если ввести в матрицу-столбец весовые коэффициенты, уравнивающие размерности отдельных составляющих. Однако такой переход не является единственным, а имеет бесчисленное количество вариантов.

Аналогичным образом при равенстве физических размерностей отдельных составляющих матриц-столбцов управляющих величин и возмущений может быть введен вектор управления и вектор возмущения. При разных физических размерностях отдельных составляющих матриц-столбцов переход к вектору возмонен, но не будет единственным.

Линеаризованные уравнения движения многомерного обтекта могут быть записаны в матричном виде:

q(p)y it) = г (р) u(t)+s (р) f (t).

Здесь введена квадратная матрица операторных коэффициентов

Яп (Р) 912 (р) - .. Qim (Р)

tr,\ II /(р) Qi2ip) qwnip)

Я КР) = II 4ji (PI \\mxm =

gml (p) q-mi. (P) q-mm (p)

И прямоугольные матрицы операторных коэффициентов

г и (р) (р) ... пи (р)

(5.67)

(5.68)

Г{Р) = \\ГП (р) mxfe =

s{P) = llSjt{p) llmxl =

ri (P) (p) rk ip)

Tml ip) Гт2 (p) - Гтк (p)

Su ip) S12 ip) ... Su (p)

S2I (P) S22 (p) . Sii ip)

Smi (p) Smi ip) Sml (p)

(5.69)

(5.70)

Если в выражениях (5.64) - (5.70) перейти к изображениям Лапласа при нулевых начальных условиях, то матричное уравнение (5.67) может быть записано для изображений в следующем виде:

Q(p)Yip) = R(p) и(р) + S ip) F (р).

(5.71)

Здесь Y (р), и (р) ш F (р) - матрицы-столбцы изображений регулируемых величин, управляющих величин и возмущений.

В уравнение (5.71) входят также квадратная матрица Q (р) = = 11 qji ip) llmxm И прямоугольные матрицы R (р) = II rji (р) JUxb

S (р) = \\ Sji (р) Wmxl-

Если матрица Q ( р) неособая, т. е. определитель \ Q (р) О, то,

умножив левую и правую части (5.71) слева на обратную матрицу (р), получим

Y (р) = Wo{p)U (р) + Wf (р) F (р). (5.72)

Здесь введены матрицы передаточных функций обтекта для управляющих величин

Q(P)

Woip) = \\Wi\\mxn = -

R{p)

и для возмущении

Wf (р) = 11 Wf ip) \u, --= s (p).

(5.73)

(5.74)

В (5.74) символом() (p) = Qji (p) \\mxm обозначена матрица, присоединенная для матрицы Q (р), а Qa (р) - алгебраическое дополнение определителя I (? (р) .

Формулы (5.72) - (5.74) позволяют получить связь между регулируемыми величинами и управляющими и возмущающими воздействиями. Так,