считая для простоты, что дифференцирующая цепь идеальна:

cos щ1-щи 1 (f) sin

(4.72)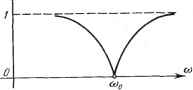

0-*-

-B. 2

Bc=-L

В результате получилось два слагаемых. Первое слагаемое является полезным, так как содержит требуемую производную от огибающей, а второе - вредным, так как оно представляет собой ложный сигнал, который может в сотни и тысячи раз превышать по уровню полезный сигнал.

Амплитудная частотная характеристика дифференцирующей /?С-цени (дифференцирующего звена с замедлением) изображена в табл. 4.7. Для получения дифференцирования огибающей модулированного

сигнала необходимо осуществить такую цепь, у которой амплитудная характеристика была бы подобна изображенной в табл. 4.7 и была бы при этом расположена симметрично относительно несущей частоты. Такая характеристика изображена на рис. 4.30, а.

Из рассмотрения характеристики следует, что звено не должно пропускать несущую частоту. Это должно быть понятным и физически, так как несущая частота в чистом виде, т. е. отсутствие боковых частот, будет при постоянном сигнале на входе

(см. (4.68)). В этом случае производная сигнала (но огибающей) будет равна нулю и на выходе звена не должно быть никакого сигнала.

При изменении сигнала по какому-либо закону, например в соответствии с выраженной! (4.69), появятся боковые частоты, которые будут пропускаться звеном тем сильнее, чем дальше они отстоят от несущей частоты, т. е. чем больше частота огибающей. Таким образом, звено будет обладать дифференцирующими свойствами но отношению к огибающей модулированного сигнала.

Амплитудная частотная характеристика, изображенная на рис. 4.30, а, может реализоваться различным образом. Такая характеристика может быть получена, например, от резонансной параллельной LC-цени, Т-образной цепи ИТ. п., настроенных на несущую частоту (рис. 4.30, б и в).

Обратимся теперь ко второй указанной выше задаче. При известной частотной передаточной функции звена w (/(о) определим эквивалентную частотную передаточную функцию wg (jq) для огибающей модулированного сигнала. Для этого вспомним, что частотная передаточная функция звена (4.17)

W (/(О) = А (ю) еЗ* = С/ (со) -f /У (со)

представляет собой комплексное число, модуль которого а (о) равен отношению амплитуд выходной и входной величин, а аргумент - сдвигу фаз при гармоническом входном сигнале в установившемся режиме. Если на входе

Рис. 4.30.

U2 (t) - Ui шах

2 2

X COSCOof+ C7i max

sincopi. (4.75)

F(a.o+Q) + y(coo-Q) .

Остановимся теперь на двух важных частных случаях.

1. Рассмотрим случай симметричной относительно несущей частоты частотной передаточной функции, что определяется равенством W [j (соо + + Q)] = W* I] (сОо - Q)], где звездочкой отмечена сопряженная комплексная величина. Из этого равенства вытекают два других: U (соо -Ь fi) = = С/ (сОо - Q) и У ((о Ч- Й) = - У (соо - О).

Тогда формула (4.75) существенно упрощается и может быть записана в виде

щ (t) = f/i шах \.и (соо + ) sin Qt + V (соо + Q) cos Qt] cos coof. (4.76)

Рассматривая огибающую, т. е. отбрасывая множитель cos сэо*, и сравнивая выражения (4.76) и (4.73), убеждаемся, что эквивалентная частотная передаточная функция для огибающей Wg (jQ) может быть получена из частотной передаточной функции звена W (/со) подстановкой со = сОо -Ь О:

Wg (/Q) = W (Усй) и=и +й = W [j (соо + Q)], (4.77)

что согласуется с полученной ранее формулой (4.71).

Так, например, если звено типа резонансного усилителя имеет частотную передаточную функцию

(/ )=l-f/(co-coo)r то передаточная функция для огибающей будет

Переход к обычной передаточной функции может быть сделан заменой jQ = р. В результате из (4.77) получаем

Wg (р) = W (/СОо + Р). (4.78)

звена действует величина {t) = Zi ах sin (at, то на выходе будет

Х (t) = Хз шах sin ((Of = шах A (ю) sin {(Ht + if) =

= шах W ((o) sin (0* + F ((o) COS CO*]. (4.73)

Для получения частотной передаточной функции по огибающей Wg (j) звена с модулированным сигналом обратимся к гармоническому сигналу по огибающей (4.69). Разложим его на боковые частоты соо + £2 и сэо - й в соответствии с выражением (4.70). Тогда, используя зависимость (4.73), получим

U2 (t) = [С/ + Q) sin (соо + Q).t + V (щ + Щ cos {щ + Q)t~

- [/(сэо -Q)sin(coo-Q)f -F(cOo-Q)cos(cOo-.Q)f], (4.74)

где и (сэ) и V (со) - вещественная и мнимая части частотной передаточной функции W (/со).

Путем разложения синусов и косинусов сумм и разностей углов это выражение преобразуется к виду

coscoof. (-4-79)

+ F(coo4-Q)-F(a.o-Q)

Так как V (со) - функция четная, [а У (со) - нечетная, то последнее выражение может быть представлено в следующем виде:

U.(t) = C/imax [±±fcsin +

+ (+ °)+(- о) cosQjcoscDof. (4.80)

В этом случае эквивалентная частотная передаточная функция для огибающей может быть определена из выражения

Аналогичный результат может быть получен, если фазочувствитель-ное устройство пропускает сигнал фиксированной фазы, например xj (f) cos (cOflf 4- ф), где ф = const. Тогда вместо выражения (4.81) получается

1Уз (;0) = (+Шо)] вФЧ-И[; (Q-Шо)] g2)

Переход к обычной передаточной функции {р) делается, как и выше, заменой jQ = р.

Формулы (4.81) и (4.82) позволяют просто находить передаточную функцию но огибающей. Однако к ним следует относиться с осторожностью. Сформулированное выше условие применимости этих формул заключалось в том, что можно было отбросить слагаемое в (4.75), пропорциональное sin (Hot, и оставить слагаемое, пропорциональное cos (Oot или в общем случае cos ((Hot + ф). Однако для этого еще недостаточно, чтобы последующее, фазо-чувствительное устройство в принципе могло отсеивать слагаемое с множителем sin (!3(,t. Необходимо, чтобы это можно было реализовать технически, для чего нужна относительная малость слагаемого с sin Oot по сравнению со слагаемым с cos о of. Только в этих условиях при имеющейся всегда нестабильности фазочувствительного устройства может быть уверенно выделено слагаемое с множителем cos со of.

В качестве примера, иллюстрирующего случай, когда формула (4.81) практически неприменима, рассмотрим опять дифференцирующую ВС-цепь (рис. 4.24, а). Примем для простоты, что ее частотная передаточная функция соответствует идеальному дифференцирующему звену W (/со) = А;;со. Тогда, в соответствии с формулой (4.81), частотная передаточная функция для огибающей будет

Это выражение показывает, что звено обладает дифференцирующими свойствами и для огибающей. Действительно, если обратиться к формуле (4.72), то видно, что при устранении слагаемого с множителем sin ©о звено

2. Рассмотрим теперь другой важный случай, когда передаточная функция W (/(о) не является симметричной , но слагаемое в формуле (4.75), определяемое множителем sin о?, отсеивается в последующих звеньях каким-либо фазочувствительным устройством, например фазовым дискриминатором. Тогда это слагаемое может быть отброшено и формула (4.74) упрощается: