Представим себе, что динамические свойства рассматриваемого звена изучаются при помогци экспериментального снятия его амплитудной частотной характеристики. Для этой цели на вход /?С-цени нужно подавать напряжение от источника с переменной частотой, например от звукового генератора, и измерять отношение амплитуд выходного и входного напряжений. Характеристика снимается только для положительных частот, а затем дополняется симметричной ветвью в области отрицатальных частот (рис. 4.28).

По отношению к амплитудной частотной характеристике можно применить следуюпций формальный прием. Входное напряжение при снятии

частотной характеристики представляет

-г-f-0 собой гармоническую функцию с угловой

частотой о и амплитудой max-

aj и,

sin Ы.

(4.65)

Используя понятие отрицательной частоты, можно представить эту функцию в виде алгебраической суммы сигнала положительной частоты и сигнала отрицательной частоты:

imax

Mi =

[sinco*-sin( -(u)f]. (4.66)

Эти сигналы называются боковыми частотами. Название произошло по сле-дуюпцей причине. Если на вход звена Рис. 4.28. поступает постоянный по величине сигнал,

то его можно представить как сигнал нулевой частоты. В этом случае коэффициент передачи звена равен ординате пересечения амплитудной характеристикой оси ординат. В рассматриваемой /?С-цепи этот коэффициент равен единице, т. е. /с = 1.

Если теперь на вход звена подать сигнал, нредставляюш;ий собой гармоническую функцию, то реакцию звена на такой сигнал можно получить, рассматривая реакцию звена на две частоты, расположенные симметрично относительно исходной нулевой частоты. Эти две частоты и являются боковыми по отношению к исходной частоте.

При наличии амплитудной частотной характеристики (рис. 4.28) постоянная времени звена может быть определена по эффекту подавления боковых частот по сравнению с исходной нулевой частотой. Из выражения для амплитудной частотной характеристики апериодического звена первого порядка (см. табл. 4.3) в общем случае, когда к = i,

следует, что на нулевой частоте коэффициент передачи звена до амнлитудо равен к, а при со = у этот коэффициент равен

\ Т } Vl + 1 У2

На основании этого соотношения по амплитудной характеристике можно легко найти постоянную времени. Для этой цели на высоте 0,707к проводится горизонтальная линия до пересечения с амплитудной характеристикой.

Абсциссы точек пересечения будут равны -= в области положительных частот

и - в области отрицательных частот.

Расстояние между точками пересечения часто называют полосой пропускания звена (4.25):

Постоянная времени может быть вычислена по полосе пропускания:

(4.67)

Обратимся теперь к звену с модулированным сигналом. Предположим, что динамические свойства некоторого звена изучаются при помощи частотных характеристик (рис. 4.29). Постоянному сигналу.на входе такого звена соответствует напряжение

Щ = max COS ©о*, (4-68)

где (Од - несущая угловая частота.

Допустим теперь, что сигнал (огибающая) изменяется по гармоническому закону с угловой частотой О. Это значит, что по гармоническому закону должна изменяться амплитуда в выражении (4.68), и модулированный сигнал может быть представлен виде

Щ = и (t) cos (Оо* = max sin qt COS (Hot,

(4.69)

sin Qt - гармонический закон изменения огибающей

где и (О = Uj, (сигнала).

Это выражение может быть преобразовано к виду

tlmax

[sin ( о -Ь ) t-sin (Ио-Q-)t].

(4.70)

Таким образом, модулированный сигнал (4.69) может быть заменен двумя гармоническими сигналами с частотами, равными сумме и разности несущей частоты и частоты огибающей: (ui = (uo-J-Qh ц} ©2 = Ио - - Эти гармонические сигналы являются боковыми частотами.

Выясним теперь, какой должна быть амплитудная частотная характеристика звена, чтобы но отношению к модулированному сигналу звено представляло собой, например, апериодическое звено первого порядка. Очевидно, что характеристика должна быть такой же самой, как характеристика апериодического звена с немодулированным сигналом, но она должна быть симметричной относительно несущейчастоты ©о (рис.4. 29). Тогда боковые частоты будут подавляться рассматриваемьш звеном так же, как они подавляются звеном с немодулированным сигналом (рис. 4.28).

Постоянную времени звена с модулированным сигналом, если оно представляет собой для огибающей апериодическое звено первого порядка, можно определить по той частоте огибающей, при которой боковые частоты подавляются в 1/2 раз.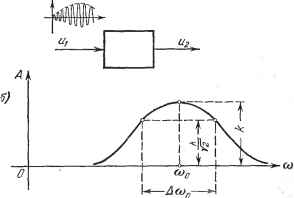

Рис. 4.29.

i+jQT

то оно должно иметь частотную передаточную функцию

Приблизительно такую передаточную функцию имеют, в частности, резонансные усилители, настроенные на несущую частоту (Oq, причем постоянная времени Т определяется полосой пропускания усилителя в соответствии с (4.67).

Проиллюстрируем применение изложенного правила на другом примере. Возьмем рассмотренную ранее дифференцирующую ЕС-цепъ (рис. 4.24, а). Эта цепь годится для дифференцирования немо дул ированного сигнала. Если на ее вход подать модулированный сигнал, то дифференцирования не получится. Действительно, рассмотрим входной сигнал щ = (t) cos Юо* где f/j {t) представляет собой закон изменения амплитуды во времени, т. е. огибающую или сам передаваемый сигнал. Продифференцируем это выражение.

Для ЭТОГО, аналогично предыдущему, на амплитудной частотной характеристике звена (рис. 4.29) должно быть сделано следующее построение. Необходимо определить коэффициент передачи звена к на несущей частоте, что соответствует постоянному входному сигналу (4.68) или частоте огибающей Q = 0. Затем на высоте 0,707А; проводится горизонтальная прямая до пересечения с частотной характеристикой и определяется полоса пропускания Дюп- Постоянная времени определяется на основании (4.67)

Рассмотренная выше методика позволяет сформулировать правило, устанавливающее требования к амплитудной частотной характеристике звена с модулированным сигналом для того, чтобы его воздействие на огибающую было таким же, каким является воздействие обычного звена заданного типа на немодулированный сигнал. Это правило сводится к следующему. Амплитудная частотная характеристика звена с модулированным сигналом должна быть такой же, как амплитудная частотная характеристика звена с немоду-лированным сигналом, но эта характеристика должна быть симметричной не относительно оси ординат, а относительно несущей частоты. Звено с немодулированный сигналом может рассматриваться при этом как частный случай звена с модулированным сигналом при несущей частоте cOq = 0.

Для того чтобы избежать ошибок в связи с наличием неминимально-фазовых звеньев, сформулированное выше правило для амплитудных характеристик должно быть дополнено аналогичным правилом для фазовых частотных характеристик. Если известно, что все рассматриваемые звенья относятся к категории минимально-фазовых звеньев, то привлечение фазовых характеристик не является необходимым и можно ограничиться использованием только амплитудных характеристик.

Таким образом, в общем случае, если обозначить эквивалентную частотную передаточную функцию по огибающей (yQ), то для частотной передаточной функции звена с модулированным сигналом W (/и) должно выполняться условие

W (/(О) = т й=а.-шо = Ij ((О - ©о)]. (4.71)

Так, например, если необходимо, чтобы по своему действию на огибающую модулированного сигнала звено соответствовало апериодическому звену первого порядка с эквивалентной частотной передаточной функцией