§ 4.8}

НЕУСТОЙЧИВЫЕ И НЕМИНИМАЛЬНО-ФАЗОВЫБ ЗВЕНЬЯ

Таким звеном может быть, например, двигатель любого тина (рис. 4.13,а) если его механическая характеристика, т. е. зависимость вращающего момента от скорости вращения М = f (О), имеет положительный наклон. На рис. 4.26 изображены разновидности механических характеристик двигателя. В случае, соответствующем кривой 1, двигатель представляет собой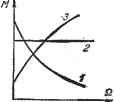

Рис. 4.25.

Рис. 4.26.

устойчивое апериодическое звено первого порядка, уравнения движения которого были рассмотрены в § 4.5. Это звено имеет положительное самовыравнивание.

В случае, соответствующем кривой 2, когда вращающий момент не зависит от скорости вращения, уравнение движения двигатсяя, записанное для угловой скорости, приобретает вид

где / - суммарный приведенный момеш инерции на валу двигателя, Ащ- коэффициент пропорциональности между управляющим воздействием и вращающим моментом. Здесь скорость двигателя связана с управляющим воздействием передаточной функцией, соответствующей .интегрирующему звену

Это звено не имеет самовыравнивания. В случае, соответствующем кривой 3, дифференциальное уравнение движения будет

dQ dt

= fcjMi -J- kiQ,

где ki - наклон механической характеристики в точке, где производится линеаризация.

Это уравнение приводится к следующему:

T-Q = kx

где Т = 1 - постоянная времени двигателя. Оно совпадает с выражением (4.56). Звено имеет отрицательное самовыравнивание.

Признаком отрицательного самовыравнивания является отрицательный знак перед самой выходной величиной в левой части дифференциального уравнения (см., например, формулу (4.56)) или появление отрицательного знака у свободного члена знаменателя передаточной функции (см., например, формулу (4.57)).

Существенной особенностью неустойчивых звеньев является наличие больших но сравнению с устойчивыми звеньями фазовых сдвигов. Так, для рассматриваемого апериодического звена с отрицательным самовыравниванием (неустойчивого) частотная передаточная функция на основ]ании (4.57)

Поэтому а. ч. X и л. а. х. этих двух звеньев (устойчивого и неустойчивого) совпадают и по одной амплитудной характеристике нельзя определить, к какому звену она относится.

Фазовый сдвиг, соответствующий неустойчивому апериодическому звену,

If = arctg = -180° + arctg

имеет большие абсолютные значения по сравнению с фазовым сдвигом устойчивого апериодического звена первого порядка (табл. 4.3): if = - arctg юГ.

В связи с этим неустойчивые звенья относятся к группе так называемых неминимально-фазовых звеньев, поскольку минимальные по абсолютному значению фазовые сдвиги при одинаковых амплитудных характеристиках будут у устойчивых звеньев. К неминимально-фазовым звеньям относятся также устойчивые звенья, имеющие в числителе передаточной функции (в правой части дифференциального уравнения) вещественные положительныекорни или комплексные корни с положительной вещественной частью. Например звено с передаточной функцией

относится к группе неминимально-фазовых звеньев. Действительно, по сравнению со звеном, имеющим передаточную функцию

оно будет иметь большие по абсолютной величине фазовые сдвиги, так как

I - arctg (uTi - arctg (иТ > arctg (лТ - arctg (иТ при одинаковом виде амплитудной частотной характеристики.

Напомним, что к минимально-фазовым звеньям относятся такие, у которых корни числителя и знаменателя передаточной функции находятся в левой полуплоскости (см. § 4.3).

К неустойчивым звеньям, кроме рассмотренного выше звена, относятся также следующие звенья с соответствующими передаточными функциями:

квазиконсервативное звено -

квазиколебательное звено -

колебательное звено! с отрицательным затуханием -

будет равна

Модуль ее не отличается от модуля частотной передаточной функции устойчивого апериодического звена (табл. 4.3):

квазиколебательное звено с отрицательным затуханием-

~л l 27p + rV неустойчивое интегрирующее звено -

(4.63)

(4.64)

и ряд других звеньев.

Наличие в автоматической системе неустойчивых звеньев вызывает некоторые особенности расчета, которые будут рассмотрены ниже (см. главу 6).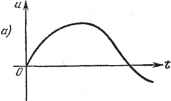

§ 4.9. Звенья с модулированным сигналом

До сих нор рассматривались звенья, в которых сигнал был немодули-рованным. В автоматических системах часто используются звенья (чувствительные элементы, усилители, серводвигатели и т. п.), у которых сигнал представляет собой неременное напряжение (или ток) некоторой частоты (Об. называемой несущей. В этом случае . закон изменения сигнала во времени характеризуется изменением амплитуды или действующего значения этого напряжения, т. е. -огибающей. На рис. 4.27 для иллюстрации приведены формы немодулированного и модулированного сигналов. Изменению знака сигнала соответствует изменение фазы несущей частоты (О о на 180°.

При расчете автоматических систем с модулированным сигналом могут возникать две задачи:

1) нахождение такого звена, которое по своему воздействию на огибающую модулированного сигнала было бы эквивалентным какому-либо обычному звену, используемому в системах с немодулированным сигналом, например апериодическому первого порядка, дифференцирующему, интегрирующему и т. п.;

2) определение воздействия звена с заданной передаточной функцией на огибающую модулированного сигнала, т. е. нахождение передаточной функции но огибающей.

Рассмотрим первую задачу. Ниже без строгих доказательств показывается путь, позволяющий сформулировать требования к частотной передаточной функции звена, чтобы его воздействие на огибающую сигнала было определенным и заранее заданным.

Для уяснения этого пути обратимся к какому-либо простейщему звену с немодулированным сигналом, например к апериодическому звену первого порядка. Для определенности в качестве такого звена возьмем ВС-цвпъ (рис. 4.13, д). Передаточная функция этого звена

Рис. 4.27.

где Т = RC.