и е). В некоторых случаях используются дифференцирующие устройства, состоящие из гидравлического демпфера и пружины (рис. 4.24, г).

-л/vv-i

Рис. 4.24.

Составим, например, уравнение для дифференцирующего конденсатора (рис. 4.24, а). Ток в рассматриваемой цепи определяется уравнением

Йг + Х J idt = Ui.

Переходя! к изображениям и решая это уравнение относительно тока, получаем:

Uiip). рС

lRCp

u.ip)

Таблица 4.6

Временные характеристики дифференцирующих звеньев

Таблица 4.7

Частотные характеристики дифференцирующих звеньев

Тип звена и его частотная передаточная функция

Амплитудно-фазовая

Амплитудная и фазовая

Логарифмические

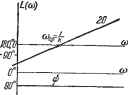Дифференцирующее с замедлением /с/со

PF(/tu)=-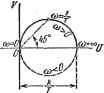

Напряжение на выходе цепи

где Т = ЯС - постоянная времени цепи.

Временные характеристики звена приведены в табл. 4.6, а частотные - в табл. 4.7.

Амплитудная частотная характеристика имеет иной вид, чем у идеального звена. Характеристики совпадают в области низких частот.-В области высоких частот реальное звено пропускает сигнал хуже, чем идеальное

звено. Коэффициент передачи стремится к значению у при и оо. Для

звеньев, представляющих собой йС- или ЕЬ-тхеш> (рис. 4.24, а ш б), к = Т и на высоких частотах коэффициент передачи стремится к единице.

Фазовые сдвиги, вносимые звеном, являются наибольшими при низких частотах. На высоких частотах фазовый сдвиг постепенно уменьшается, стремясь в пределе к нулю при со оо. Здесь также видно, что это звено ведет себя подобно идеальному только в области низких частот.

Л. а. X. строится по выражению

L (со) = 20 Ig , . (4.55)

Асимптотическая л. а. х. может быть представлена в виде двух прямых. Одна из них имеет положительный наклон 20 дб/дек (при со < 1/Г), а вторая- параллельна оси частот (при со > 1/Т).

§ 4.8. Неустойчивые и неминимально-фазовые звенья

Рассмотренные выше звенья позиционного типа относятся к устойчивым звеньям, или к звеньям с самовыравниванием. Под самовыравниванием понимается способность звена самопроизвольно приходить к новому установившемуся значению при ограниченном изменении входной величины или возмущающего воздействия. Термин самовыравнивание обычно применяется для звеньев, представляющих собой объекты регулирования.

Существуют звенья, у которых ограниченное изменение входной величины или возмущающего воздействия не вызывает прихода звена к новому установившемуся состоянию, а выходная величина имеет тенденцию неограниченного возрастания во времени. К таким звеньям относятся, например, звенья интегрирующего типа. Они были рассмотрены выше.

Существуют звенья, у которых этот процесс выражен еще заметнее. Это объясняется наличием положительных вещественных корней или комплексных корней с положительной вещественной частью в характеристическом уравнении (знаменателе передаточной функции, приравненном нулю), в результате чего звено будет относиться к категории кеустпойчмвмх звеньев. Вопрос устойчивости будет изложен подробно в главе 6. Рассмотрим в качестве примера звено, описываемое дифференциальньш уравнением

Т-Х2==кхи (4.56)

которому соответствует передаточная функция

Переходная функция. такого звена представляет собой показательную функцию с положительным показателем степени:

h{t) = k{eT-i).l{t). (4.58)

Эта функция изображена на рис. 4.25.