суммируется с напряжением щ. Эта сумма и представляет собой выходное напряжение и.

Таким образом, для схемы, изображенной на рис. 4.22,je,

где Т - коэффициент пропорциональности между скоростью изменения выходного напряжения датчика интегрирующего привода и напряжением

Таблица 4.4

Временные характеристики интегрирующих звеньев

Тип звена и передаточная функция

Переходная функция

Функция веса

Идеальное

W{p) = -

w(t) = k-l{t)

С замедлением

W{p)=-

P(i + Tp)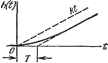

h{t) = h[t-T{i-e

w{t) = k{\ - e )-l{f)

Изодромное

k{i+Tp)

h(t)

-A -V

h{t) = (kt+ki).i{t)

w(t)

т{Р) = кЛЩ\ЬЩ

на его входе. Коэффициент передачи идеального интегрирующего звена в этом

, 1 случае равен л; = у.

Временные характеристики звена представлены в табл. 4.4, а частотные - в табл. 4.5.

Л. а. X. строится по выражению

L(co) = 201gL!I±.

Асимптотическая л. а. х. представляет собой две прямые: с отрицательным наклоном 20 дб1дек при (о <; и параллельную оси частот при и > y-j.

Таблица 4.5

Частотные хараастеристаки йвтегрйруюьтк звеньев

Тип звена и частотная передаточная функция

Амплитудно-фазовая

Амплитудная и фазовая

Логарифмические

Идеальное

W{im) =

Интегрирующее с замедпеЕием к

/й)(1+/(оГ)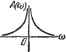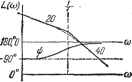

Изодромное

wu.)=-X+k,jlj

а(а>)

>гг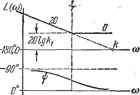

вательно, = В режиме, близком к хо-

лостому ходу (сопротивление нагрузки ве- ~ - -

лико), можно считать, что напряжение якоря

равно э. д. с: и = е. Тогда и = /с .

Приближенно в качестве идеального дифференцирующего звена может рассматриваться операционный усилитель в режиме дифференцирования <рис. 4.23, б).

Временные характеристики приведены в табл. 4.6, а частотные - в табл. 4.7.

2. Дифферет1(ирующее звено с замедлением. Звено описывается уравнением

Передаточная функция звена

Звено условно можно представить в виде двух включенных последовательно звеньев - идеального дифференцирующего и апериодического первого порядка.

На рис. 4.24 изображены примеры дифференцирующих звеньев с замедлением. Наиболее часто употребляются электрические цепи (рис. 4.24, а, б

Из рассмотрения л. а. х. и л. ф. х. видно, что в области малых частот (меньших, чем сопрягающая частота) звено ведет себя как идеальное интегрирующее и тем точнее, чем меньше частота.

В области больших частот (больших, чем сопрягающая частота) звено ведет себя как безынерционное с коэффициентом передачи к.

Свойство звена вводить интегрирующее действие в области малых частот используется для улучшения качественных показателей систем автоматического регулирования (см. главу 9).

§ 4.7. Дифференцирующие звенья

1. Идеальное дифференцирующее звено. Звено описывается уравнением

2 = к-. (4.51)

Передаточная функция звена .

W (р) = кр. (40.52)

Примеры идеальных дифференцирующих звеньев изображены на рис. 4.23. Единственным идеальным дифференцирующим звеном, которое точно описывается уравнением (4.51), является тахо-

генератор постоянного тока (рис. 4.23, а), т - -

если в качестве входной величины рассма-

тривать угол поворота его ротора а, а в ка-

честве выходной - э. д. с. якоря е. В тахо- -fi

генераторе постоянного тока при неизменном потоке возбуждения э. д. с. в якоре пропорциональна скорости вращения: е = Ш. ffj Скорость вращения есть производная по f I I

о da I -1-Ц уХ-а

времени от угла поворота: У = -тт. Следо-