Продолжение табл. 4.3

Тип звена и частотная передаточная функция

Амплитудно-фазовая

Амплитудная и фазовая

Логарифмические

Колебательное W (;м) =

1 + 7

A(w)

у1(Сй) =

V(l-Сй2Г2)2 42(д2у2 2СйГ

Консервативное TF(/cu)=-

то 1

-Ч Q -10

-180

if) = 0 при - 5<со<;5, ,),= -180° при сй>д, il)= -f-180° при м< -5.

г01дк

выбрать нормированную п. а. х., соответствующую данному значению , ПОДНЯТЬ ее параллельно самой себе на 20 Ig и по оси частот от относительной частоты перейти к действительной умножением на q.

В функции той же относительной частоты на рис. 4.18 нанесены нормированные л. ф. X., построенные по выражению

If =-arctg-(4.41)

Построение л. а. х. колебательного звена можно делать также посредством проведения двух асимптот с наклонами О и 4f) дб1дек, пересекающихся 1

в точке (й = -, с последующим введением поправки, которая приведена на рис. 4.19.

Нормированные переходные характеристики колебательного звена для случая к=\. приведены на рис. 4.20 в функции относительного времени qt.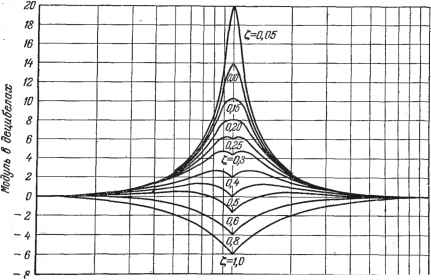

0 0,4 0,5 OJB 0,8 1,0 Z

Относительная частота

Рис. 4.19.

S 6 8 10

Сравнение рис. 4.18 и 4.20 показывает, что снижение параметра затухания приводит к повьппению колебательности переходного процесса и росту резонансного пика амплитудной частотной характеристики.

5. Консервативное звено. Консервативное звено является частным случаем колебательного при t = 0. Тогда передаточная функция (4.35) будет иметь вид

W-(/) = -l + 2

(4.42)

Консервативное звено представляет собой идеализированный случай, когда можно пренебречь влиянием рассеяния энергии в звене. Для изображенных на рис. 4.17 примеров мы получим консервативные звенья, есл1

в случаях а) и б) положить Л = О, в случае в) положить 5 = О и в случае г) положить F = 0.

Временные характеристики соответствуют незатухающим колебаниям (табл. 4.2) (угловой частотой q.

Частотные характеристики приведены в табл. 4.3. При частоте (й = д модуль частотной передаточной функции обращается в бесконечность., а фаза делает скачок на 180°.

0 1 2 3 4 5 в Рис. 4.20.

7 8 yf=f

Амплитудно-фазовая характеристика совпадает с вещественной осью. При О <; <; g характеристика совпадает с положительной полуосью, а при (£> > q - с отрицательной полуосью.

§ 4.6. Интегрирующие звенья

1. Идеальное интегрирующее звено. Звено описывается дифференциальным уравнением

= kxi.

Передаточная функция звена

(4.43) (4.44)

Такое звено является идеализацией реальных интегрирующих звеньев, часть которых будет рассмотрена ниже. Примеры интегрирующих звеньев приведены на рис. 4.21. Часто в качестве такого звена используется операционный усилитель в режиме интегрирования (рис. 4.21, а). Интегрирующим звеном является также обычный гидравлический демпфер (рис. 4.21, б). Входной величиной здесь является сила F, действующая на порщень, а выходной - перемещение порпгая Xz- Так как скорость движения поршня пропорциональна приложенной силе (без учета инерционных сил):

dx Ж