более быстро, чтобы можно было выявить свойства объекта в текущий момент времени. С другой стороны, все указанные выше методы требуют некоторого конечного времени, определяемого необходимостью накопления сигналов на фоне шумов. Так, например, при корреляционном методе время самонастройки обычно значительно превышает время переходного процесса, определяемое по затуханию весовой функции (25.30).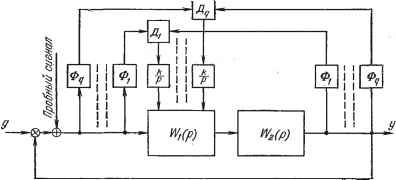

Рис. 25.12.

На рис. 25.12 в качестве примера изображена схема самонастраивающейся системы с определением амплитудных частотных характеристик. Работа схемы происходит следующим образом. На вход системы поступает пробный сигнал, содержащий фиксированные частоты ш, . . ., <Вд. Эти частоты на входе и выходе системы выделяются узкополосными фильтрами Ф, а затем в делительных устройствах Д происходит деление выходной амплитуды на входную. Это дает фиксированные точки амплитудной частотной характеристики (или л. а. х.) на пробных частотах со, . . ., <Вд. В случае отклонения частотной характеристики от заданного значения сигнал с выхода делительного устройства поступает через усилитель на исполнительный элемент, представляющий собой интегратор, который воздействует на корректирующее устройство с целью восстановления требуемого значения модуля частотной передаточной функции на данной частоте.

Нетрудно видеть, что процесс самонастройки в этой системе в некотором роде подобен автоматическому синтезу системы регулирования по ее частотным характеристикам. Число дискретных частот пробного сигнала определяется сложностью регулируемого объекта. Оно совпадает с числом опорных точек логарифмической амплитудной характеристики, которое надо иметь, чтобы осуществить синтез системы по методу л.а. х.

Таким образом, самонастраивающиеся системы этого типа (рис. 25.11) представляют собой, по существу, устройства автоматического синтеза систем регулирования по заданным качественным показателям.

Системы с экстремальной самонастройкой. Эти системы отличаются от рассмотренных выше систем с замкнутыми цепями самонастройки тем, что в них автоматически осуществляется оптимальный синтез системы автоматического регулирования. Структурная схема в этом случае совпадает со схемой, изображенной на рис. 25.11.

Для реализации оптимального синтеза в основу работы вычислительного устройства должен быть положен некоторый критерий оптимальности. При расчете систем автоматического регулирования часто используется критерий минимума среднеквадратичной ошибки, когда минимизируется

средний квадрат опшбки:

ж2 = Ит4г ( xdt. (25.31)

Очевидно, что реализовать эту оценку для самонастраивающейся системы затруднительно. Это связано, во-первых, с тем, что необходимо вычисление интеграла (25.31) в бесконечных пределах, и, во-вторых, с тем, что оценка остается неизменной во все время работы системы.

Практически легко реализуется минимизация оценки вида

t t-x

F= J ж2(т)е dr. (25.32)

Устройство, реализующее выражение (25.32), представляет собой квадратор (звено, возводящее входную величину в квадрат) и последовательно включенное апериодическое звено с постоянной времени Т. Функция веса такого звена

t

w{t) = e

Выходная величина этого устройства, записанная при помощи интеграла Дюамеля, совпадает с (25.32).

Постоянная времени Т апериодического звена, которое является фильтром нижних частот, должна выбираться так, чтобы устройства изменения параметров корректирующего звена практически не реагировали на случайные быстрые изменения ошибки х.

Системы с экстремальной самонастройкой являются наиболее совершенными самонастраивающимися системами. Они обеспечивают оптимальную настройку системы в условиях изменения характеристик объекта, регулятора и возмущающих сил. Однако они являются наиболее сложными системами и их реализация сталкивается пока со значительными техническими трудностями.

Самонастраивающиеся системы с экстремальной настройкой относятся к категории экстремальных систем с поиском минимума или максимума некоторой величины, определяющей оптимум работы системы. В качестве регулируемых величин i/i, . . ., i/ здесь выступают параметры корректирующего устройства, например общий коэффициент усиления, значения постоянных времени и передаточных коэффициентов и т. п. Исследование этих систем может производиться в соответствии с теорией экстремальных систем (§ 25.1).

Системы с самоорганизацией. Самоорганизующиеся системы по своей первоначальной структуре представляют собой набор элементов, связанных между собой случайным образом.

В дальнейшем при внепших возмущениях в них образуются устойчивые отрицательные и положительные обратные связи, подобно тому как в природе происходит приспособление живых организмов к различным внешним условиям. Для живых организмов также характерны отрицательные обратные связи, в результате которых эти организмы уравновешивают неблагоприятные внешние воздействия, и положительные обратные связи, усиливающие благоприятные воздействия.

Самоорганизующимся системам свойственна большая универсальность (приспособляемость) и большая надежность по сравнению с обычными системами.

Самоорганизующиеся системы еще не получили распространения, и работа с ними не выходит пока из стадии первых опытов. Так, например.

В литературе [47] описывается моделирование на математической машине ИБМ-704 процесса поиска методов решения новой задачи. В машину вводилось много различных программ, в том числе бессмысленные, и ставилась задача. Машина решала задачу наугад, чаще всего неправильно. Результат решения оценивался, и на основе оценки изменялся метод решения. После нескольких сотен тысяч попыток у машины накопился опыт и появилось суждение о правильном методе решения. В дальнейшем она придерживалась этого метода, несколько изменяя его, если изменялись условия.

Задача, которая ставилась машине, состояла в обработке 14-значного числа посредством 63 математических операций. Авторы эксперимента считают, что проще построить машину, способную самостоятельно выработать методику решения, чем точно составить алгоритмы этого решения.

Опыты с самоорганизующимися системами, несомненно, могут принести большую пользу конструкторам сложных систем управления, так как высшая стадия развития жизни на Земле - человек,- по сути дела, возникла на основе принципов самоорганизации неживой природы. Использование этих принципов может привести к весьма совершенным, надежным и универсальным системам управления.

Игровые системы. Игровые системы используются для управления различного рода операциями и, в частности, военными операцияьш. Игра или борьба может вестись против организованного противника или против сил природы (случайного процесса).

. На рис. 25.13 изображена структурная схема игровой системы. Управляющая машина этой системы имеет так называемый игровой алгоритм. Он заключается в сравнении возможных в данной обстановке решений

Управляемая операция (tcm оран а)

Информация о состоянии управляемой операции

Действия противнина (2сторона)

Инфортци о действиях противника

Управляющая

машина с игровым алгоритмом

Система передачи т.тнд

Рис. 25.13.

и выборе из большого числа решений оптимального. После принятия реше- ния управляющая машина должна сформировать и передать к управляемой операции команды управления.

Сравнение вариантов решений делается управляющей мешмной на основе заложенных в нее критериев. Эти критерии выражаются в виде некоторой функции, которую называют функцией выгоды. Установление рациональной функции представляет собой основную проблему при построении игровых систем.

При исследовании игровых систем в настоящее время используется специальная математическая дисциплина - теория игр. Главным содержанием теории игр является обоснование так называемых оптимальных стратегий ведения игры.