в общем случае наличия нескольких переменных. . ., Уп) потери на поиск определяются суммой

(25.18)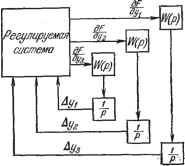

Рассмотрим исследование динамики экстремальной системы при F-,- = F {уу, . . ., у ) для случая поиска экстремума по способу градиента. Структурная схема для этого случая изображена на рис. 25.5.

Вместо (25.13) здесь будут иметь место более сложные зависимости:

yi = -W(j>)-~: (i = l,2, ..., ) (25.19) или, в ином виде,

.( = 1.2, ...,п), (25.20)

где W (р) - передаточная функция, одинаковая для всех каналов. Рис. 25.5.

Для малых отклонений от точки экс-трегдума разность F - F может быть представлена в виде квадратичной формы:

-= = 4- S г ДУгА№, (25.21)

в и-мерном пространстве координат (Ai/i, ..., Ai/ ) поверхность

S aiuAyiAy = i (25.23)

г, fe=l

ДЛЯ экстремума-минимума представляет собой эллипсоид, называемый определяющим эллипсоидом. Поверхность

2 Ayi Дуь = - 1

i, fe=l

(25.24)

соответствует определяющему эллипсоиду экстремума-максимума.

в теории квадратичных форм показывается, что для малых отклонений уравения (25.20) могут быть записаны в виде

Ауг = ±Ау (г=1,2, ...,п),

(25.25)

где Ci - полуоси определяющего эллипсоида. Знак плюс соответствует минимуму и знак минус - максимуму.

Из (25.25) получаются характеристические уравнения для каналов:

i-+i=o.

(25.26)

Здесь знак введен в передаточную функцию W {р), которая должна быть положительной для экстремума-максимума.

Таким образом, исследование динамики при F = F {у-, . . ., Уп) сведется к анализу п изолированных каналов, которым соответствуют характеристические уравнения (25.26).

Рассмотрим теперь систему с шаговым поиском. На рис. 25.6 изображена схема шагового поиска максимального значения функции (у). В регулируемом объекте эта функция должна превращаться в напряжение постоянного тока Uy по линейной или иной зависимости. Схема осуществляет поиск максимального значения Uy.

Изменение регулируемой величины у осуществляется серводвигателем Д. Работа всей схемы происходит при помощи управления от временного программного устройства, которое в определенной последовательности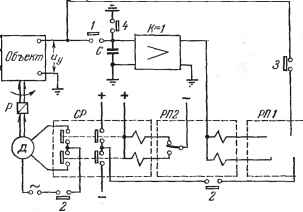

Рис. 25.6.

заьшкает свои контакты. Эти контакты пронумерованы цифрами, помещенными рядом. В соответствии с последовательной работой программного устройства рассмотрим работу схемы.

1-е положение. Замыкается контакт 1, который на короткое время включает конденсатор С. Конденсатор заряжается до значения напряжения Uy. Далее при размыкании контакта 1 это напряжение запоминается на конденсаторе. К нему подключен усилитель с большим входным сопротивлением и коэффициентом усиления, равным единице. Выходное напряжение ус1шителя будет равно запомненному на конденсаторе напряжению Uy.

2-е положение. Замыкаются контакты 2. Один из них включает на короткое время силовое реле СР, которое подводит напряжение к реверсируемому серводвигателю Д. В результате регулируемая величина изменится на определенное значение Ьу, т. е. система сделает один шаг . Второй контакт 2 также на короткое время подключает к напряжению источника постоянного тока обмотку поляризованного реле РП1. Это делается для того, чтобы поляризованное реле запомнило направление шага.

В начале работы схемы положение поляризованного реле РП2 может быть произБольньви. Поэтому трехпозиционное силовое реле может включаться в произвольную сторону, и шаг для поиска экстремума делается также Б произвольную сторону.

3-е положен и е. Замыкается на короткое время контакт 3, который включает обмотку реле РП2 на разность напряжений Uy до и после шага. Если напряжение Uy уве-личилось после шага, реле РП2 остается включенным Б прежнем положении. Если это напряжение уменьшилось, реле РП2 переключится в другое положение и подготовит включение силового реле Б следующем цик.ле в другую сторону.

Это остается справедливым и в том случае, когда контакт реле PII2 включен не наверх, как показано на рис. 25.5, а вниз.

4-е п о л о ж е н и е. На короткое время замыкается контакт 4, который замыкает конденсатор С и стирает записанное (запомненное) на нем напряжение Uy. Тем самым схема подготавли-

Шеш ИЭ

Рис. 25.7.

вается для следующего цикла работы, который протекает аналогично.

На рис. 25.7 изображена структурная схема рассмотренной экстремальной системы. Значение регулируемой величины, соответствующее точке экстремума, обозначено у. В схему

введен импульсный элемент ИЭ, соответствующий шаговому характеру работы схемы, и нелинейный элемент НЭ. Наличие нелинейного элемента вызвано тем обстоятельством, что величина шага системы постоянна и меняется только направление самого шага. Это и обеспечивается нелинейным элементом с идеальной релейной характеристикой.

Серводвигатель совместно с регулирующим органом, изменяющим значение регулируемой величины, представлен в виде некоторой непрерывной части (р). Непрерывным звеном является также сам объект регулирования Wi (р).

Процессы в данной экстремальной системе могут изучаться при помоп1;и моделирования структурной схемы (рис. 25.6). Могут использоваться также аналитические методы исследования нелинейных импульсных систем.

Как следует из структурной схемы, в системе весьма вероятны автоколебания около точки экстремума. Это объясняется тем, что звено с идеальной релейной характеристикой при малых входных сигналах имеет коэффициент передачи, стремящийся к бесконечности. Поэтому и этой схеме будут присущи потери на поиск в соответствии с формулой (25.17).

§ 25.2. Самонастраивающиеся системы

Самонастраивающиеся системы регулирования должны обеспечивать необходимое качество процессов регулирования при изменении свойств объекта регулирования и элементов регулятора, а также при изменении характеристик возмущающих сил.

В отличие от экстремальных (поисковых) систем здесь самонастройка часто осуществляется аналитическим путем без организации процесса поиска.

Самонастраивающиеся системы подобного типа называют беспоисковыми. Теория самонастраивающихся систем изложена в работах [30, 52, 85].

Системы с разомкнутыми цепями 1 самонастройки. Эти системы используются в практике уже сравнительно большое время. Структурная схема подобной системы изображена на рис. 25.8. Здесь Wy и обозначают передаточные функции части системы. Пусть - передаточная функция объекта и регулятора, а Wy - передаточная функция некоторого звена, которое будем называть корректирующим устройством.

Под влиянием внешних возмущений Д, . . ., / происходит изменение передаточной функции W-

Рис. 25.8.