НИИ, близком К мгновенному направлению вектора градиента (непрерывно или дискретно).

В простейшем случае непрерьтного безынерционного управления для этого должны реализовьшаться зависимости

dF dF

(25.13)

где к - некоторый коэффициент пропорциональности. Заметим, что для получения правильного направления движения должно быть й > О для случая экстремума-максимума и /с <С О для экстремума-минимума.

Траектория движения изображающ;ей точки у,. . ., Уп в этом случае оказывается нормальной к поверхности F (у, . . ., i/ ) = const.

Уравнения (25.13) соответствуют устойчивому движению экстремальной системы, так как из (25.12) следует

dF dt

(25.14)

Следовательно, производная функции F по времени сохраняет свой знак (больше нуля при /с > О и меньше нуля при к <: 0) повсюду, кроме точки экстремума, где эта производная обращ;ается в нуль, что соответствует монотонному сходящемуся процессу.

При шаговом движении реализуются зависимости

л J dF

Ауп = к

(25.15)

Ау1, . . ., Ауп - фХШсированные шаги в направлении экстремума. Для способа градиента характерно плавное движение по направлению к точке экстремума и малый размах колебаний около точки экстремума при шаговом движении.

Способ наискорейшего спуска. При способе наискорейшего спуска движение происходит по нача.льному направлению вектора градиента F до тех пор, пока производная функции по этому направлению не обратится в нуль. Затем опять определяется направление градиента и происходит движение вдоль этого вектора до обращения в нуль производной от F по этому направлению. Процесс повторяется до достижения точки экстремума.

Этот способ характеризуется быстрым выходом системы в район экстремума, что делает его предпочтительным для начальной стадии движения. В районе экстремума можно использовать другие способы, например способ градиента.

На рис. 25.2 для случая двух регулируемых величин, что соответствует F = F (уг, у), изображены траектории движения для рассмотренных выше способов поиска экстремума [61]. Кривая 1 соответствует способу Гаусса - Зайделя, кривая 2 - способу градиента и кривая 3 - способу наискорейшего спуска.

Рассмотрим теперь пример экстремальной системы для наиболее простого случая, когда F = F (у).

Пример. На рис. 25.3 изобраншна схема экстремального регулирования настройки колебательного контура. Полезный сигнал с частотой / поступает на параллельный резонансный контур, состоящий из катушки L

и конденсаторов переменной емкости Су и Cg. Конденсатор имеет сравнительно небольшую емкость. Ротор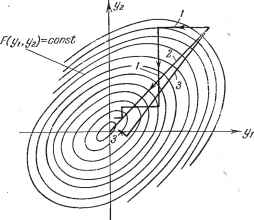

L 1/т

Рис. 25.2.

Рис. 25.3.

его вращается двигателем постоянной скоростью, вызывая периодические изменения общей емкости контура, которая является регулируемой величиной.

Общая емкость колебательного контура

С = Су + С Су + Со + Ау sin щи

где - постоянная составляющая емкости конденсатора С, а cOj - угловая скорость вращения его ротора.

Частота cOj выбирается так, чтобы она была во много раз меньше частоты полезного сигнала со = 2л/ и больше возможной частоты процесса регулирования.

Двигатель Д2 синхронно с вращением ротора конденсатора дает опорную величину в синхронный детектор СД, например, в виде опорного напряжения той же частоты от генератора ГОН.

Переменное напряжение на колебательном контуре после выпрямления и сглаживания фильтром Фу поступает на вход синхронного детектора. На выходе синхронного детектора формируется сигнал, пропорциональный

производной от амплитуды напряжения контура по емкости Этот сигнал

после сглаживания фильтром Фзюступает далее на усилитель и двигатель Д1. Последний будет вращать ротор конденсатора Су, т. е. изменять регулируемую величину и производить подстройку контура до тех пор, пока производная не станет равной нулю. Всякое изменение частоты сигнала / будет

вызывать автоматическую подстройку на максимум напряжения на контуре.

В этой системе поиски экстремума по способам Гаусса - Зайделя, градиента и наискорейшего спуска сливаются в один вследствие наличия только одной регулируемой величины (емкости контура).

Нетрудно видеть, что в рассмотренной экстремальной системе получается своеобразная следящая система, ошибкой в которой является производ-

АС,

нг,р

1 системах.

р(Мр)

Помимо обычных показателей качества для экстремальных систем используется еще одна характеристика - потери

РИС. 25.4.

В установившемся режиме регулируемая величина колеблется около значения, соответствующего экстремуму функции F (у). Вследствие этого среднее значение этой функции отличается от экстремального. Среднее значение разности F - Fq, обусловленное колебаниями поиска в установившемся режиме работы системы, назьтается потерями на поиск.

Поскольку в точке экстремума первая производная = О, то разность

между текущим и экстремальным значениями функции F (у) можно представить Б виде степенного ряда

- = Т(Д)+-(Д)+--- (25.16)

Здесь частные производные соответствуют точке экстремума, а - отклонение от этой точки. Если в (25.16) можно ограничиться только первым членом ряда, т. е. использовать квадратичную форму, то потери на поиск можно представить в виде

= i- (25-17)

где Ду2 средний квадрат отклонения регулируемой величины от значения Уэ, соответствующего экстремуму.

При гармоническом поиске с амплитудой средний квадрат Др = .

пая в соответствии с этим структурная схема этой экстремальной систе-

мы может быть сведена к структурной схеме следян];ей системы (рис. 25.4).

Входной величиной является значение емкости Сд, соответствующее экстремуму. Это значение связано с частотой полезного сигнала со и индуктивностью приближенным соотношением (при пренебрежении влиянием активных сопротивлений)

В контур структурной схемы входят апериодические звенья, соответствующие фильтрам 01 и Фз, и интегрирующее звено с замедлением (двигатель Д). Результирующая передаточная функция разомкнутой системы

где Т - электромеханическая постоянная времени двигателя, и - постоянные времени фильтров.

На рис. 25.4 Показано также воздействие / от неподавленной переменной составляющей на выходе синхронного детектора и воздействие ДСд, представляющее собой помеху во входном сигнале.

Как следует из рис. 25.4, исследование динамики рассматриваемой экстремальной системы сводится к исследованию следящей системы. Поэтому здесь применимы все методы, используемые Б непрерывных автоматических