г л А в А 25

АДАПТИВНЫЕ СИСТЕМЫ

§ 25.1. Системы экстремального регулирования

Системами экст/)ежо1ького регулирования называются системы, в которых задающие воздействия, т. е. заданные значения регулируемых величин, определяются автоматически в соответствии с экстремумом-(максимумом или минимумом) некоторой функции F {уу, у, у, . . ., jr ). Эта функция зависит не только от регулируемых величин у, . . ., г/ , но и от неконтролируемых параметров системы и времени t. Поэтому она не является постоянной и заранее известной. Однако изменение функции F и смещение экстремальных значений регулируемых величин уу = у, у = у, . . ., Уп= Упэ протекает относительно медленно.

Условием экстремума дифференцируемой функции нескольких переменных F {уу, у2, . - ., Уп) является равенство нулю в точке экстремума частных производных этой функции:

-1 = 0, -1 = 0, ...,-1 = 0. (25.1)

Градиентом функции F называется векторная величина

g-<ii-i- + + (25.2)

где Kl, . . ., Кп - единичные векторы осей, по которым отсчитываются величины У1, . . ., Уп-

В точке экстремума градиент равен нулю:

grad F = 0. . (25.3)

Задача поиска экстремума разбивается на две:

1) определение градиента;

2) организация движения в точке экстремума.

Для решения как первой, так и второй задачи предложено много способов. Ниже будут рассмотрены только простейшие из них [61]. Обратимся сначала к задаче определения градиента.

Способ синхронного детектирования. Способ основан на том, что к основным медленно меняющимся величинам 1, . . ., у добавляются малые гармонические (в общем случае периодические) составляющие:

Уг

(25.4)

чае периодические; (

1 = y + Al sin (Oit, i = у1 + А sin wt.

Уп = Уп + An sin (Out.

Величина (1, . . ., поступает на синхронные детекторы (рис. 25.1), у которых в качестве опорных величин испо.льзуются те же переменные составляющие (25.4). Идеальные синхронные детекторы умножают величину F на переключающую функцию, представляющую собой прямоугольную

волну с периодом Tt = 2л/со,- (г = sir(o,l = 1, 2, . . ., ?г) и высотой единица.

1 sina}f Переключающая функция прибли-

женно может быть заменена синусои-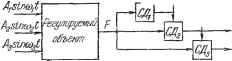

Рис. 25.1.

£1пщг f дой частоты и j с единичной ампли-тудой. Поэтому средние значения Ug выходных величин синхронных детекторов . . ., Un приближенно могут быть представлены в виде

щ = F sin (si-it, = F sin att, . . .

..., Un = F sin (i)nt.

В квазистационарном режиме, когда составляющие уЧ меняются медленно по сравнению с поисковым движением At sin cOj-, величины щ, . . ., Un с точностью до малых высших порядков пропорциональны соответствующшм

dF dF n

частным производным - в точке Уг = ifi, = у1, , Уп =

= Уп И, следовательно, определяют grad F в этой точке.

Для доказательства этого разложим функцию F в окрестностях точки

f, . ., Упв степенной ряд:

F{y\ + yi, ...,yn + yn)F{f ...,i/) + 2 Аг/г +

, 1 dF> . . , 1 v(

+-2Г S -duxyy+w S

г, k=i

dFO dyi dyji dy,

УiУky+... (25.5)

в последнем выражении значения частных производных соответствуют точке у1, . . ., I/? а Ау = Ai sin (ot, . . ., Ауп = А sin (dnt.

Выходные величины синхронных детекторов можно представить в виде

Ug = F sin oigt = F yn) sin (Hgt +Аг sin cojt sin cogf --

+-- 2 AiAhsin(i>itsin(i>htsin(i>qt + ... (25.6)

i, fi=l

Если величины jrj, . . ., y постоянны или меняются настолько медленно, что их изменениями за небольшой период можно пренебречь, то, учитывая очевидные равенства:

sin cogi = 0.

sin (Oft sin (Hqt = - {i = q), sin coj sin cogi = 0 (iq),

выражение (25.6) можно свести к виду

1 . dFo

ДМд.

(25.7)

(25.8)

+Ж 2 AiAkAv jsm Wit sm (i>kt sin (i>.,t sm (i>gt + ... (25.9)

i, ft, v=l

Величина Aug no отношению к амплитдам Aj, . . ., An имеет порядок малости не ниже третьего, а по сравнению с Uq - не нине второго. Если частоты выбраны по закону нечетных чисел со = (2i + 1) >о, где cOq = = const, то удовлетворяются условия coj ф а {i фк) vi (di ± а>и ф± сОд. Тогда

. sin cOjf sin cofei sin cogi = О (25.10)

и величина JS.Uq имеет порядок малости не ниже четвертого.

Таким образом, выходные величины синхронных детекторов с достаточной степенью точности можно считать пропорциональными состаБЛяющ;им градиента F в точке i/J, . . ., т

Способ производной по времени. Производная по времени функции F (Ух, . . ., Уп) определяется выражением

dF dF dyi , dF dyn

dt dyi dt

(25.12)

Отсюда следует, что, задавая поочередно скорости изменения у, . . ., Уп

И измеряя производную по времени можно найти составляюп1,ие градиента (25.3). Некоторым недостатком этого метода является необходимость дифференцирования функции F по времени, что сопровождается поднятием уровня высокочастотных помех.

Способ запоминания экстремума. Этот способ заключается в том, что система совершает вьшужденное или автоколебательное движение в районе экстремума. При достижении экстремального значения F = Fg оно фиксируется на запоминающем устройстве. Градиент функции определяется затем по разности текущего и экстремального значений F - Fg.

Обратимся теперь к организации движения по направлению к экстремуму. Рассмотрим несколько возможных способов.

Способ Гаусса - Зайделя. Способ заключается в поочередном изменении координат Уу, . . ., yj. Сначала фиксируются все координаты у, ... . . ., Уп, а координата уу изменяется так, чтобы обратилась в нуль соответ-

ствующая составляющая градиента т-. Затем изменяется координата у

при фиксированных остальных координатах до обращения в нуль v- и т. д.

После изменения координаты уп обращаются опять к уу и далее повторяют весь цикл снова. Этот процесс продолжают до тех пор, пока не будет достигнута точка экстремума F.

Этот способ не обеспечивает быстрейшего достижения точки экстремума вследствие того, что координаты изменяются не все разу, а поочередно.

Способ градиента. В этом способе осуществляется одновременное изменение всех координат так, чтобы обеспечить движение системы в направле-

Погрешнбсть метода определяется членом Дмд, которому соответствует выражение

1 Ч-1 dio

Auq=Y Zj fed-dfe smco;smcOfesmcOg-f

i, h=i