Это выражение можно упростить, если учесть, что fi=--! при v = 0 и fi- - -AJ при всех остальных значениях v. Тогда

-l[y+A-(i-A)¥ -*] =

2IV-1 . я

-3-1 v-.

так как сумма членов вида е при v = О, 1, . . ., 2А - 1 равна нулю. Из (24.120) получается нормированный коэффициент гармонической линеаризации

(24.121)

Расчет параметров периодического режима, когда Лср = - целое число, не представляет труда. По значению опшбки в установившемся режиме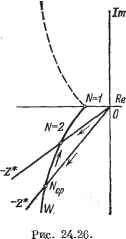

m+i т

---п---о-.

Рис. 24.27.

определяется относительный полупериод колебаний N (24.118). Затем из (24.76) находится амплитуда колебаний на выходе системы:

Я1 =

(24.122)

где определяется формулой (24.106). На рис. 24.26 показано графхгческое построение для А=2. Если Ар представляет собой дробное число, то колебания носят квазипериодический характер. Их приближенный расчет может быть сделан следующими методами.

1) Введем предположение, что при переходе от одного периодического режима с целым значением = Ло к другому с новым целым значением N = Nf, -{- 1 амплитуда первой гармоники и частота усредненного периодического режима изменяются непрерывно и плавно. В части частоты колебаний это полностью подтверждается формулой (24.116). Тогда для расчета амплитуды первой гармоники колебаний можно воспользоваться тем же графическим построением (рис. 24.26) и формулами (24.116) и (24.122) при замене в последней N на Лср и со на == nN.

2) Второй метод заключается в том, что для усредненного значения х [п], изображенного на рис. 24.27, а с учетом действия экстраполятора (пунктирная линия), находится обычными приемами разлоишния в ряд Фурье аьшлй-туда первой гармоники

(24.123)

Ci = - sm-

2iV,

Далее может быть определена амплитуда колебаний на выходе системы пересчетом Су на вход (умножением на 6) и умножением на модуль частотной передаточной функции разомкнутой системы:

Здесь

= eiCiW(eJ oT)=sm

(24 124)

С0о =

г 2 (ОоГ

(24.125)

- круговая частота и псевдочастота периодического режима (частота преобладающей гармоники)

3) Возможно использование способа расчета, когда рассматривается некоторый дополнительный усредненный режим движения у* (t) на выходе непрерывной части (рис. 24.27, б), полученный припасовыванием на интервалах времени 0-ТжТТо = 2NcpT. Далее в случае необходимости можно выделить в этом режиме первую гармонику. В отличие от предьщущих двух методов, здесь расчет может производиться и в тех случаях, когда время существования на выходе экстраполятора сигнала {т -\- I) b не подчиняется условию TVi = 1, а может содержать произвольное число тактов.

Пример. Пусть передаточная функция непрерьшной части

Woip) = -

(24.126)

Дискретная частотная передаточная функция разомкнутой системы

(24.127)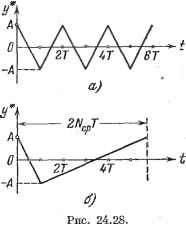

где К = оц - общий коэффициент усиления разомкнутой цепи с присоединенньш коэффициентом передачи ЦВМ (24.73).

Режим симметричных колебаний при ж* = 0,5б1построеннарис. 24.28, а. Амплитуда может быть найдена методом припасовывания:

6i КТ

(24.128)

Так как из условий устойчивости КТ < 2, то < 0,56i. Относительный полупериод А = 1. Первая гармоника этого колебательного режима имеет амплитуду

6i КТ 26iKT

ai =

(24.129)

Первая гармоника может быть также найдена из (24.103) для (ИдТ = я

а,=АИ*(Уоо):

(24.130)

что близко совпадает с (24.129).

Рассмотрим теперь несимметричные колебания. Зависимость Ncp от установившегося значения ошибки Хд в соответствии с (24.114) и (24.118)

представлена на рис. 24.29. Точками отмечены целочисленгше значения TVcp-

Воспользуемся первым изложенным методом. В соответствии с (24.122)

6 5 4 3 2 iV

i 1J5 Рис. 24.29.

-sin

(24.131)

При 7Vcp>2 формула (24.131) дает

При использовании второго метода в соответствии с (24.124)

sm -

(24.132)

(24.133)

При iV > 2 формула (24.133) переходит в (24.132).

Для того чтобы воспользоваться третьим методом, рассмотрим средний цикл колебаний. Он построен методом припасовьшания для выходной величины на рис. 24.28, б. Алшлитуда колебаний

2 Же

Амплитуда первой гармоники при разложении в Фурье

-jt2(2iVcp-l) 2iVcp

6,КТ 2iVcp

(24.134)

(24.135)

ПОЛНОСТЬЮ совпадает со значением (24.131).

Все полученные вьфажения для амплитуды первой гармоники показывают сравнительное постоянство ее для различных значений Аср.