С учетом коэффициента усиления нелинейной части выбран на основании формул (24.42) и (24.43):

<Т- (24-93)

где М - допустимое значение показателя колебательности.

Получим теперь условие отсутствия периодических режимов для типовых л. а. X., изображенных па рис. 24.19. Рассмотрим наиболее тяжелый случай системы с астатизмом второго порядка (рис. 24.19, в). Для доказательства определим условие, при котором фазовая характеристика не будет заходить в соответствующие запретные зоны на фиксированных частотах (24.89). Запишем зто условие следующим образом:

~л-Ь-<ф(Х), . (24.94)

где

Формулу (24.94) можно представить в следующем виде:

-л+-<-л + arctg Iq-T2~2 arctg - J + arct g У. ( - ) (24.95)

Для частот, лежапщх левее частоты среза {N = 3, 4, 5, . . .), формулу {24.95) с достаточной точностью можно привести к виду

.<arctgtg-- (24.96)

-.-<arctg-tg. (24.97)

Учитывая, что N 3, и используя (24.21), получим из (24.97) простое условие отсутствия периодических режимов:

1<А~ . (24 98)

Последнее неравенство вьшолняется при М 2.

Рассмотрим теперь случаи 7V = 1 и 7V = 2. При N = I частота периодического режима Q = я/Г, а абсолютная псевдочастота -> оо. Однако на частоте оо запретная область для фазовой характеристики отсут-

ствует (рис. 24.19), что говорит о невозможности существования периодического режима.

При N = 2 частота периодического режима Q = я/2 Г, а абсолютная псевдочастота Xq = 2/Т. Запретная зона на частоте % = 2/Т также отсутствует (рис. 24.19), что говорит о невозможности существования периодических режимов и на этой частоте.

Фазовые характеристики для типовых л. а. х. (рис. 24.19, а и б) в области низких частот отстоят от запретной области дальше, чем у рассмотренной выше л. а. х., соответствующей астатизму второго порядка. Поэтому полученное выше условие невозможности появления периодических режимов будет справедливым и для л. а. х. этих типов.

Симметричные периодические режимы. Несмотря на то, что в согласованном положении можно добиться отсутствия периодических режимов.

В системах с ЦВМ периодические режимы, вызванные квантованием по уровню, будут существовать практически всегда. Это объясняется, тем, что при наличии ненулевой установившейся ошибки начальная точка статической

/!}

Рис. 24.21.

характеристики входного преобразователя смещается из начала координат в другую точку (рис. 24.21, а)

Если начало отсчета сместилось в точку 1, то это не дает отличия в получаемой характеристике от исходного случая равенства нулю входного и выходного сигналов. Если начало отсчета сместится в точку 2, то результирующая статическая характерно- х. тика будет иметь вид, изображенный на рис. 24.21, б. д-i-i-i-,-,-,-, l i 7-

Требуемое дробное значение выходной величины преобразователя х -0,5-может быть получено только в результате периодического переключения от уровня т + I к уровню т

и обратно. Это будет симметричный периодический режим, относительный полупериод которого может быть различным: 7V = 1, 2, 3, ...

Системы с ЦВМ стараются делать так, чтобы амплитуда симметричного периодического режима на превышала единицы младшего разряда [67]. Тогда в подобном режиме входная величина ЦВМ (сигнал опшбки) будет представлять собой периодическую решетчатую функцию, изображенную на рис. 24.22. Для этого случая нелинейная зависимость для входного преобразователя может быть записана в виде (см. рис. 24.21, б).

Рис. 24.22.

X* sign ж*,

(24.99)

где X* - переменная составляющая ошибки, вызванная периодическим режимом, а ж* - ее цифровое представление.

Для определения коэффициента гармонической линеаризации необходимо положить ж* [п] = Cicos -f (pj, где - ф1< I . Далее,используя формулу (24.84) и для приведения к безразмерному виду вводя в соответствии с (24.69) нормируюпщй множитель = получим для случая N = I из (24.88)

(24.100)

Амплитудно-фазовые характеристики величины - Z* изображены на рис. 24.23, а. Они представляют собой прямые, расположенные во втором и третьем квадрантах.

Для случая = 2 аналогичным образом можно получить

- Z* = <

(о>ф.>-).

(24.101)

Амплитудно-фазовые характеристики представляют собой прямые линии,

расположенные в секторе - 180°+ 1т

± 45° (рис. 24.23, б).

При = 3 модуль \Z* \ =

= 15 . Характеристики расположены в секторе - 180° + 30° (рис. 24.23, в).

Для > 3

Z* -.-g-, (24.102)

причем характеристики расположены в секторе - 180° dz N . 90° (рис. 24.23, г). При Nоо, что соответствует непрерывному случаю, сектор расположения а. ф. X. стягивается в линию, совпадающую с отрицательной вещественной полуосью.

Уравнение периодического режима имеет вид (24.76). Его можно решить графически (рис. 24.17) или аналитически. В последнем случае необходимо приравнять - Z* = W. В результате при наличии точки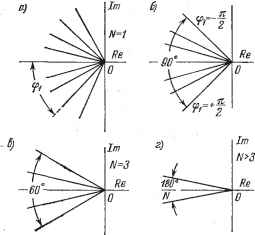

Рис. 24.23.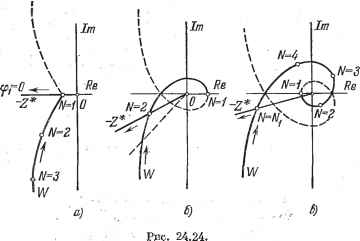

пересечения, как это показано, например, на рис. 24.24, а, для = 1 амплитуда ошибки или, что все равно, амплитуда регулируемой величины