Тип звена и его передаточная функция

Переходная функция h (t)

Функция веса w (г)

Безынерционное W(p) = k

fi(t)

h(t) = k-\ {t)

w(t)=k-S{t)

Апериодическое 1-го порядка

W{p)=-

1+Tp

h(t) = k(i-e )-l{t)

Апериодическое 2-го порядка

W{p)

i + TiP+np\

(1 + УзРИ1 + УзР)

3,4 =

(Г1>2Г2; Ts>Ti)

Г,-TV Tfy

h{t) = k

Г3-Г4

Г3-Г4

Колебательное W(p) =

i + 2t,Tp+Tp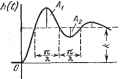

Y = - 111--+ ,

fc(i) = fc 1 -e-* cosXг-f ---smXJ -1(f)

31 iJo

(f) = -+- e-* sin Xf-l (/)

Таблица 4.2

Временные характеристики позиционных звеньев

Продолжение табл. 4.2

Тип звена и его передаточная функция

Переходная функция h (t)

Функция веса w (t)

Консервативное к

5 = -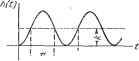

h(t)=k(l-cos gt).l {t)

m(t)

i\yi

Ш (i) = kq sin gi-1 (i)

Л. a. X. строится no выражению L (со) = 20 Ig

(4.39)

Однако построение л. a. x. не может быть сделано так просто, как это было для предыдущих звеньев. Для построения используются так называемые нормированные л. а. х. Постоянный множитель под знаком логарифма в выражении (4.39) может быть выделен в отдельное слагаемое:.

L(co)=201gA;-f 201g- . (4.40)

Построение первого слагаемого (4.40) не представляет никакого труда. Второе 2D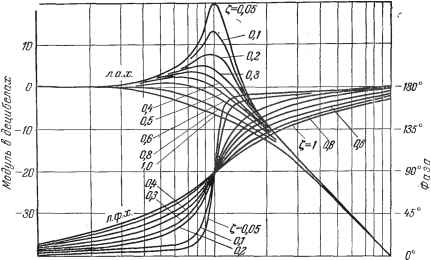

0,4 0 0,8 t г 2

Относительная частота

Рис. 4.18.

3 4

6 8 Ю oo/(j=<ji>T

слагаемое может быть построено в функции относительной частоты - для

различных значений параметра затухания 1, в виде универсальных (нормированных) кривых (рис. 4.18). Для построения истинной л. а. х. необходимо

Таблица 4.3

Частотные характеристики позиционных звеньев

Тип звена и частотная передаточная фзгнкция

Амплитудно-фазовая

Амплитудная и фазовая

Логарифмические

Б езынерционное

у4(м) = /с, il) = 0

Апериодическое 1-го порядка к

W(i(i>) =

1+/МТ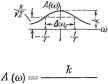

L(o>)

Vl+Wya

, ij3(co)= - arctg шГ

Апериодическое 2-го порядка к

(1-+-7шГз)(1+/ Г4)

tI80°

A (и) == , -,. ,

1/1+йУ! 1/1+иУ!

ф (со) = - arctg шГз-arctg С0Г4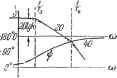