Тогда на его выходе получим сигнал

Ж2 [п] = / {Xi М) = i- 2 ке , (24.82)

где А; = rh 1, ± 3, . . ., +Z, причем I = 7V, если N нечетно, и Z = 7V - 1, если N четно.

Коэффициенты этого тригонометрического полинома выражаются формулой Бесселя [114] (см. также § 15.2)

fe, = Ъп/ = .А 2 / (1 [1) (2-83)

Если N нечетно, то при k = N

bN = 4[2i f(iM)e- -. (24.84)

v==0

Далее, как это следует из метода гармонической линеаризации, нужно ограничиться в (24.82) учетом лишь первой гармоники, т. е. использовать гипотезу фильтра. Для системы регулирования с ЦВМ .определение периодических режимов при N = I я N = 2 может быть произведено точно. Из (24.82) следует:

для N = 1

Х2 [п] = by cos (яп), (24.85)

где fei = / ( 1 cos Ф1);

для TV = 2

a;2[n] = feiC0S n-f . (24.86)

Комплексная амплитуда

by = byeSi = f {ay cos ф) - / (% cos ф) e 2.

При TV >- 3 определим приближенное значение х [п], учитывая только первую гармонику:

Ж2 [п] feicos n-blij . (24.87)

Условию существования периодических режимов соответствуют

Y* ( 1, ф1, N) = 0./ >

Поскольку возможные частоты периодических режимов находятся в целочисленном отношении с частотой выдачи данных ЦВМ, то уравнения (24.80) позволяют отыскивать амплитуду и фазу фх-

Рассмотрим порядок определения коэффициентов гармонической линеаризации для нелинейной зависимости = f (ж).

Пусть ко входу нелинейного элемента с симметричной характеристикой приложено гармоническое воздействие, заданное своими дискретными значениями:

Xi [п] = ai cos (-n-f Ф1) [J+e~\ (24.81)

Комплексная амплитуда

Отношение [n] к arj [n] в комплексной форме дает выражение для Коэффициента гармонической линеаризации:

JV-1

й1 aie

Рис. 24.18.

2 /[a.cos(v + T,)]e~(--). (24.88)

Сложная зависимость коэффициентов гармонической линеаризации не только от амплитуды а, но и от сдвига фаз а также относительного полупериода N приводит к значительной трудоемкости определения перио-дЕгаеских режимов в системе регулирования с ЦВМ. Дополнительные осложнения вознхгоают при попытке определить устойчивость периодических

режимов. Однако при постановке задачи синтеза обычно не ставится вопрос об отыскании периодических режимов. Наоборот, может быть поставлена задача так синтезировать систему регулирования с ЦВМ, чтобы исключить возмоншость возникновения периодических режимов в согласованном положении системы регулирования при . I Жует I < 0,5 6i, где 6i - цена младшего разряда входного преобразователя.

Рассмотрим, каким образом необходимо учитывать квантование по уровню, если синтез системы регулирования вести на базе типовых желаемых л. а. х. При этом наибольший интерес представляет случай одноразрядного выходного преобразователя, которому соответствует максимальное отклонение характеристики преобразователя от линейной зависимости.

Если ограничитвся случаем невозможности возникновения периодических режимов (рис. 24.17), то вместо годографа величины -Z* (%, ф1, N) необходимо построить огибающую области, где расположены все возможные кривые - Z* при различных значениях N = const, ф; = const и = var.

В результате построения можно показать [131], что запретной областью

для годографа величины W (У;] с некоторым запасом является сектор

(рис. 24.18) с углом раствора у = nIN, вне зависимости от принятого числа раарядов рассматриваемой нелинейной характеристики.

Периодические режимы в системе будут невозможны, если амплитудно-фазовая характеристика линейной части системы, построепная по функции W (У;) на фиксированных относительных частотах со = лШ (абсолютная частота со = лШТ) не будет заходить в запретную область.

При достаточно больших значениях относительного полупериода N, т. е. при малых частотах, q* (а, Ц), N) -q(.aj) и годограф нелинейной части стремится к годографу соответствующей нелинейности в непрерьтной системе регулирования.

Для отыскания условий невозможности появления периодических режимов в согласованном положении [131] обратимся к типовым л. а. х. (рис. 24.10). Эти л. а. X. построены на рис. 24.19. Там же нанесены запретные области для фазовых характеристик аналогично тому, как это было сделано на рис. 8.30. Запретные зоны построены симметрично относительно фазового сдвига

ф = -180°. Высота запретных зон в угловой мере связана с частотой искомых периодических решений Q = nINT. При N = i высота запретной зоны равна 180°, при N = 2 равна 90°, при N = Ъ равна 60° и т. д.

Для исключения периодических режимов фазовая характеристика {Ц на фиксированных частотах

[(24.89)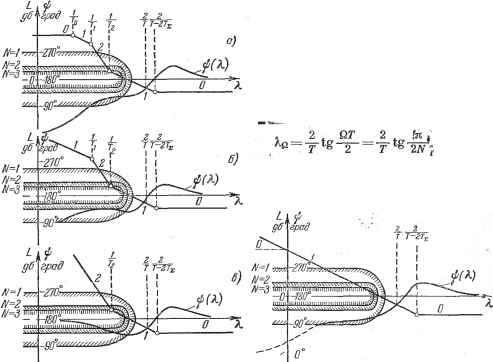

не должна заходить в запретные зоны, построенные для этого же значения

Рис. 24.19.

Рис. 24.20.

N = const. Если фазовая характеристика на фиксированной частоте (24.89) будет находиться в запретной зоне, соответствуюгцей тому же значению N, то возможно сугцествование периодического режима с частотой Q = nINT.

Рассмотрим вначале л. а. х. несимметричного вида (рис. 24.20), которой соответствует передаточная функция непрерывной части

(24.90)

Соответствующая дискретная частотная передаточная функция имеет вид

Г V Г. . I Т

W* (jK) =

z(l A)[l+A(.J r);

A(i+A-2-)

(24.91)

Сопоставление фазовой характеристики я]) (тс) и запретных зон (рис. 24.20) показывает, что периодические режимы при рассматриваемых типах нелинейностей невозможны, если общий коэффициент усиления разомкнутой цепЕ