где ба - цена младшего разряда. Число отличных от нуля уровней характеристики, если 2 - число двоичных разрядов преобразователя, будет

fXa = 2 2 1. (24.72)

Обычно 6i = 62, ki = ж fii = (Хг.

Объединенная статическая характеристика входного преобразователя для канала ошибки показана на рис. 24.15, в. По оси абсцисс отложена

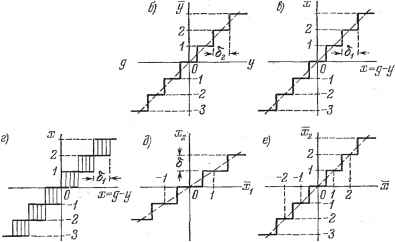Рис. 24.15.

опшбка X = g - у, а по оси ординат - ее цифровое представление х. Характеристика справедлива для случая, когда задаюп];ее воздействие g = тЬу = - const, где т - целое число, либо у = тб = const. Первый случай рассматривается обычно при исследовании периодических ренчимов, вызванных квантованием по уровню.

В общеж случае статическая зависимость х = f (х) определяет область расположения характеристик, которая показана на рис. 24.15, г. Характеристика, изображенная на рис. 24.15, в, представляет собой, по сути, некоторую среднюю характеристику этой области.

На рис. 24.15, д изображена статическая характеристика выходного преобразователя. По оси абсцисс отложена выходная величина ЦВМ в виде цифры Ж], а по оси ординат х, - выходная величина преобразователя Д - Н совместно с экстраполятором. Обычно эта величина представляет собой электрическое напряжение или ток. Единица младшего разряда для выходной величины Х2 обозначена б.

Крутизна линеаризованной характеристики будет здесь к = 6. Если D (z) = 1 или lim D (z) = 1 при z 1 (в установившемся режиме), то обилий линеаризованный коэффициент передачи ЦВМ совместно с входным и выходным преобразователями будет

(24.73)

кц - kjjt - -т .

Для этого случая на рис. 24.15, е изображена результируюш;ая статическая характеристика ЦВМ совместно с преобразователями в относительном (цифровом) виде, т. е. х, = f (х).

Если число двоичных разрядов выходного преобразователя а, то общее число отличных от нуля уровней статической характеристикибуцет

fx = 2 - 1. (24.74)

На рис. 24.16 изображены статические характеристики при а = 1, 2 и 3 для случая, когда максимальное значение выходной величины одно и то же.

Наличие рассмотренных нелинейностей в ЦВМ может вызвать периодические режимы в С1ютеме регулирования. В случае их устойчивости получаются автоколебания. Однако термин автоколебания здесь несколько

-6 -о -4 -3 -2 -/

. S

J I . I-

-J-1-1-1-(-1-

i Z 3 4 ё В

Рис. 24.16.

условен, так как частота периодических режимов жестко связана с частотой выдачи данных ЦВМ.

При исследовании периодических режимов, вызванных квантованием по уровню [137], можно воспользоваться методом гармонической линеаризации, изложенным в главе 18.

Однако следует сделать предварительные замечания. Если Z) (z) 1, то статические характеристики входного и выходного преобразователей могут быть объединены в одну (piro. 24.15, е). Тогда получается система с одним нелинейным звеном, которая может быть исследована достаточно просто.

Если D (z) ф \ ъ том смысле, что в ЦВМ вводится некоторая корректирующая программа (см. § 24.3), то получаются, вообще говоря, два нелинейных звена, разделенных линейными фильтрами. Исследование подобных систем оказывается более сложным.

Однако при наличии корректирующей программы D {z) ф\ можно выделить частный случай, когда при поступлении на вход ЦВМ целого числа х на выходе ее будет также пеокругляемое целое число х. В зтом случае выходная величина ЦВМ будет точно попадать на линеаризованную характеристику (рис. 2АЛ5, д), что эквивалентно исчезновению влияния одной нелинейности в пределах отсутствия насыщения выходного преобразователя.

Примером такой корректирующей программы ЦВМ может служить приведенная в табл. 24.2 передаточная функция

Z)(z) = -J .i

Если А ш в - целые числа, а А - В вие будет выполняться.

4 = A-Bz-K

1, то сформулированное выше уело-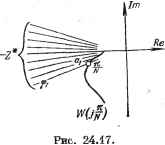

В дальнейшем изложении будет рассматриваться только случай, когда две нелинейности сводятся к одной, отнесенной ко входу ЦВМ.

Рассмотрим условия существования периодических режимов в системе регулирования с ЦВМ. Согласно методу гармонической линеаризации приближенное уравнение периодического режима можно представить в виде

1 +g*W = 0. (24.75)

где q* - коэффициент гармонической линеаризации нелинейного элемента (входного устройства ЦВМ) но первой гармонике при учете квантования по времени в нормированном (безразмерном) виде, W = DW° - дискретная частотная передаточная функция линейной части системы в разомкнутом состоянии.

В уравнении (24.75) предполагается, что коэффициент передачи входного устройства присоединен к линейной части и рассматривается нелинейность единичного вида (см. рис. 24.15, е).

В отличие от коэффициентов гармонической линеаризации непрерывных систем (см. главу 18), коэффициент q* зависит не только от амплитуды на входе нелинейного элемента но и от фазы входного воздействия

и частоты воздействия со = соГ = где N = Ту12Т - относительный

полупериод. Таким образом, q* = q* {а, ф, N). В результате уравнение периодического режима (24.75) приобретает вид

l + 9*( i,9i,iV)Pr(/-)=0 Л

или . > (24.76)

( 1) = -idr ( J

Частота периодического режима Q находится в целочисленном соотношении с частотой выдачи данных ЦВМ 2л/Т. Таким образом, все возможные

частоты периодических режимов заранее известны.

Определение периодических режимов можно производить несколькими способами.

Возможно совместное рассмотрение годографа дискретной частотной передаточной функции линейной части WiJnlN) и графиков - Z* (а, ф, N), что показано на рис. 24.17. Точка пересечения при л/iV = (для данного N) указывает амплитуду % и фазу периодического режима. Можно пользоваться и обратными характеристиками. .Возможно использование кривых Михайлова. Для этого целесообразно представить коэффициент гармонической линеаризации в виде

q* к, Ф1, ЛО = ? к, Ф1, N) + jq (%, ф1, N). (24.77)

Уравнение характеристической кривой будет

D* (/-, ai, щ) =<?(/:)+Д (l-) [?(ai, Ф1, N) + iq ( i, Ф1, Щ\. (24.78) Выделим в выражении (24.78) вещественную и мнимую части:

аи Ф1) = X* -f /У*, (24.79)

где коэффициенты X* и Y* зависят от ф и iV.