Л. а. X. для нее построена на рис. 24.9, а.

На этом же рисунке построена запретная зона для л. а. х. на основании условий по точности и в соответствии с рис. 12.11. Базовая частота (12.76)

Требуемое значение общего коэффициента усиления при совпадении первой асимптоты л. а. х. с границей запретной зоны (рис. 12.24)

со = сок = 150 сек-.

В соответствии с расчетом, проделанным выше, для л. а. х., изображенной на рис. 12.14 и рис. 24.7, получаем требуемое значение постоянной времени

-==i/S=lb /S5 = °12 сеп. Частота среза л. а. х.

= Kxi = СОо yl = 12,2 4l = 21,2 сек-К

В соответствии с формулой (24.41) получаем далее -2-<7-=2ТТ21ХГ1 = 284 сек,

откуда допустимый период дискретности Г 0,0568 сек. В случае учета постоянных времени Т-, и Гд имеем

1г< -ЩТл -+ 2 + Т,) = 0,0284-0,013 = 0,0154 сек

и допустимый период дискретности Т 0,0308 сек.

Аналогичные расчеты для случая ikf = 1,2 дают = 0,2 сек, cogp = = 30 и Т < 0,0368 сек (при 7, = 7 = Гд = 0) и 7 < 0,026 сек (при

1\ 0, У, 0 и Т, фО).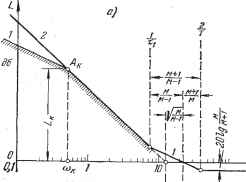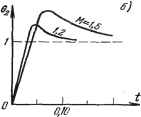

о,го сек

Рис. 24.9.

На рис. 24.9, б для иллюстрации ностроеныТнереходные процессы при воздействии на входе в виде едшичной ступенчатой функции. Переходные процессы построены посредством разложения в ряд Лорана z-преобразования выходной величины.

Таким образом, синтез следягцих систем методом л. а. х. на основе частотных критериев качества (по точности и запасу устойчивости) оказывается применимьж и для систем, содержащих в своем контуре ЦВМ. При этом все расчеты сохраняют свою простоту и наглядность.

Для расчета удобно применять абсолютную псевдочастоту, которая в области низких частот (левее частоты среза) совпадает с обычной угловой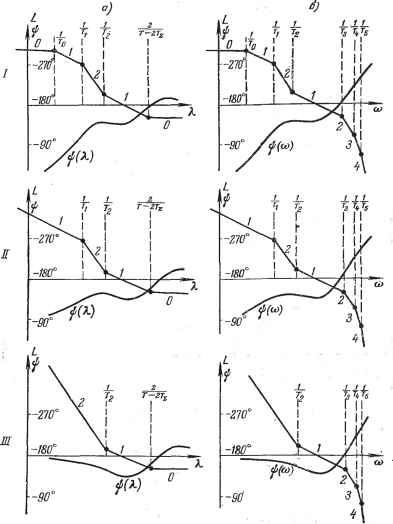

Рис. 24.10.

частотой со. При этом в области высоких частот л. а. х. приходится строить по сумме малых постоянных времени. Влияние квантования по времени, вносимое ЦВМ, легко учитывается при построении только л. а. х., без необходимости рассмотрения фазовой характериСтхши.

Для облегчения процесса синтеза можно ввести понятие типовых л. а. X. систем регулирования с ЦВМ. На рис. 24.10, а приведены типовые л. а. X. для статической системы и астатической первого и второго порядков без учета временного запаздывания. На рис. 24.10, б изображен

соответствуюшде им л. а: х. непрерывной части, а в табл. 24.1 приведены передаточные функции.

Таблица 24.1

Типовые передаточные функции

Тип п.а.х.

Степень астатизма

Дискретная частотная передаточная функция

Передаточная функция непрерывной части

к (l + Afg) (l-A )

(i+m (i+Ari)

x;i+A(4-r,);

х[1+/я(4-г,)]

XUl + T-oP) (l + riP)X Х(1 + ГзР).-.(1+2,.р)...}-1

щ1+адх

X{p(l-[-rjP) (1-[-7зр)Х х(1-1-Т4Р)...(1 + Ггр)...}-

(1+Г2Р)Х

Х{р8(1 + Гзр) (1 + Г4Р)..-

...(1 + Ггр)...}-*

Синтез непрерьшных корректирующих средств. При использовании для коррекции системы непрерывных средств возможно применение корректирующих средств трех основных видов: последовательных, параллельных и обратных связей (рис. 10.1). Наиболее просто производится расчет корректирующих средств последовательного типа. В этом случае дискретная передаточная функция разомкнутой системы должна равняться желаемой передаточной функции

Иж (Z) = W\W, iz). (24.47)

Здесь ИпкПо (2) представляет собой дискретную передаточную функцию последовательно включенных корректирующего звена с передаточной функцией W\k ip) и непрерывной части с передаточной функцией Wo (р). Напомним, что Ппко (z) ф Ипк (z) Wq (z). Поэтому расчет последовательных корректирующих средств в дискретных системах не является столь простой задачей, как в непрерывных системах.

Однако выше было показано, что л. а. х. дискретных систем, построен-

ные в функции абсолютной псевдочастоты ?i, = - tg-g- для частот К<с2/Т

практически сливаются с л. а. х. непрерывной части. Поэтому можно воспользоваться известными приемами расчета последовательных корректирующих средств, если в качестве желаемых л. а. х. использовать характеристики, соответствующие передаточным, функциям непрерывной части.