Результирующий фазовый сдвиг

1, = -180° 2 arctg %Tj - 2 arctg iTt -

3=1 i=l

- 2 arctgX ~ -b arctg Я - ) - (24.39)

В районе частоты среза при X<i 2/Т можно считать с достаточной точностью

- 180°-Ь 2 arctgЯт;- 2 arctgЯУг - arctgX {+ У) . (24.40)

3=1 г=1

В результате при построении высокочастотного хвоста приходится учитывать сумму малых постоянных времени Тх и дополнителышй множитель (1 - ]ХТ/2). Последний приводит к подъему л. а. х. на высоких частотах и дает дополнительный фазовый сдвиг в отрицательную сторону, равный arctg кТ/2. Методика расчета следяпщх систем с ЦВМ и здесь совпадает с методикой расчета непрерывных систем, изложенной выше. Только формула (12.96) должна быть переписана в виде

i+ S <1-Щл- (24.41).

i=g+l

Аналогичным образом для несимметричных л. а. х. типа 1-2-3 . . . (рис. 12.18) систем с астатизмом первого порядка можно показать, что вид. л. а. X. в низкочастотной области сохраняется, а требуемый запас устойчивости получится при

+2,< ii±ZOEi (м<1,3). (24.42),

Последнее выражение является достаточным, если имеется хотя бы одна постоянная времени, по величине большая чем Т/2. Если для всех постоянных врем:ени вьшолняется условие Т <; Т/2, то для предотвращения захода высокочастотного хвоста л. а. х. в запретную зону (рис. 12.16) необходимо выполнить дополнительное условие

При построении л. а. х. для систем с ЦВМ можно не вводить специального обозначения для псевдочастоты X, а употреблять обычное обозначение со,.

Начало л. а. х. в высокочастотной области сливается с концом л. а. х.. низкочастотной области в точке % = сОср-

При построении фазовой характеристики следует учитывать появление множителя (1 - ]%Т/2), соответствующего неминимально-фазовому звену. Для построения фазовой характеристики можно воспользоваться результирующим выражением для дискретной частотной передаточной функции, которое на основании изложенного будет

Z(l-bATi) ... (1-ьАт ) иц) [i+jX W*{i%) =----1А, (24.38).

считая, что В области рабочих частот (левее частоты среза) это есть частота входного воздействия, а в высокочастотной области она переходит в псевдочастоту.

Сделаем теперь два замечания. Первое относится к случаю наличия в передаточной функции непрерывной части (24.25) сомножителей, [соответствующих колебательным звеньям с передаточной функцией

Если выполняется условие qT <; 2, то дискретная частотная передаточная функция для подобного сомножителя совпадает с частотной передаточной функцией непрерывного звена и она может быть получена подстановкой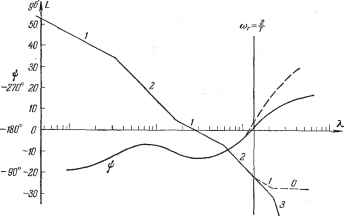

Рис. 24.8.

р = ik и умножением на (1 - ]%Т/2). При qT > 2 построение л. а. х. несколько усложняется вследствие явления транспонирования частот. Однако и здесь не возникает никаких принципиальных трудностей [10].

Второе замечание касается последней части условия 2, которое было сформулировано вьппе при построении л. а. х. для передаточной функции (24.25). Если для всех постоянных времени Tq+i . . . Тп условие Ti <; 0,ЪТ не вьшолняется, то построение л. а. х. делается следующим образом. Строится л. а. X., соответствующая передаточной функции непрерывной части (рисунок 24.8). Затем проводится вертикальная линия, соответствующая гранич-2

ной частоте сОр = у. Л. а. х., расположенная левее граничной частоты,

соответствует низкочастотной части, и она может быть принята в качестве л. а. X. дискретной системы, так как в этой области абсолютная псевдочастота совпадает с обычной частотой X л; со.

Далее находится формула, соответствующая высокочастотной части л. а. X. непрерывной системы, аналогичная формуле (24.33). Пусть, например, пересечение граничной частоты происходит при наклоне асимптоты 40 8б1дек так, как это показано на рис. 24.8. Тогда уравнение высокочастотной части будет

где в = - частота пересечения оси частот асимптотой, имеющей отрицательный наклон 40 дб/дек.

ной части

W%{iX)=---Ц---LL, (24.45)

Tx = Ti + T+ ...+Tn,

n=Tl+...+n + TiT + TJTs +...+TyTn + TTb +...

Если выполняется условие < Г, то формула (24.45) упрощается:

Wt (А) ---. (24.46)

В соответствии с выражением для (Щ строится высокочастотная часть л. а. х., которая показана на рис. 24.8 пунктиром.

Построение фазовой характеристики делается аналогично изложенному выше.

Таким же способом строится высокочастотная часть л. а. х. при пересечении граничной частоты асимптотой 60 дб/дек, 80 дб/дек и т. д. Во всех случаях формирование высокочастотной части делается по сумме малых постоянных времени, которьш соответствуют сопрягающие частоты, находящиеся правее граничной частоты сОр = 2/7.

Пример. Произведем расчет следящей системы с астатизмом второго порядка при следуюшдх исходных данных:

1). максимальная входная скорость fimax = Ю град/сек;

2) максимальное входное ускорение вшах = 5 град/сек;

3) максимальная допустимая ошибка бщах == 2 угл. мин.;

4) непрерывная часть содержит постоянные времени Ту = 0,01 сек, = 0,002 сек и Ts = 0,001 сек;

5) допустимый показатель колебательности М = 1,5 и М = 1,2. Требуется определить параметры непрерывной части системы и допустимый период повторения ЦВМ.

Решим задачу вначале для случая Ту = Т = Тд = О и М = 1,5. Передаточная функция непрерывной части разомкнутой системы, структурно устойчивой в замкнутом состоянии, должна иметь вид

где Ту - постоянная времени, вносимая корректирующим звеном дифференцирующего типа.

Так как высокочастотная часть после частоты среза в рассматриваемом идеализированном случае представляет собой прямую с наклоном 20 дб/дек, то вся частотная передаточная функция системы с ЦВМ может быть получена подстановкой р = Ja, где to - псевдочастота, и введением дополнитель-го множителя (1 - jwT/2):

K{i+}aai)(i-ja~) оО--)=--

Раскладывая выражение (24.44) на простые дроби, переходя к Wb (z), а затем к (/Х), получим аналогично формуле (24.36) для высокочастот-