т. е. ошибку X = g - у. В функции этой ошибки ЦВМ должна прикладывать к системе регулирования Рис. 24.4. . . управляющее воздействие. Поэтому

для исследования динамики следует пользоваться структурной схемой (рис. 24.4), в которой ЦВМ условно введена последовательно в цепь вычисления ошибки. В общем случае в контуре регулирования мон?ет присутствовать элемент чистого временного запаздывания, выделенный в отдельное звено с передаточной функцией е~Р.

Эффекты запоминания на период интегрирования весовой фушщии (рис. 24.3), определяемые формулами (24.1) и (24.3), учитываются также отдельным . звеном с передаточной функцией

где Z = еР.

Если кроме определения ошибки х = g - у ЦВМ производит интегро-дифференциальные операции, то в контуре будет также присутствовать дискретная передаточная функция D (z), соответствующая некоторому дискретному фильтру, разностное уравнение которого может быть получено и D (z) на основании (15.96) и (15.98).

Ключи, изображенные на структурной схеме (рис. 24.4), генерируют ийшульсные функции в соответствии с периодом повторения ЦВМ. Проходя через запоминающее устройство (24.12), последовательность ийшульсных функций образует ступенчатую функцию (рис. 24.3).

Рассмотрим теперь простейшие примеры.

Пример 1. Пусть непрерывная часть системы регулирования соответствует астатизму первого порядка и представляет собой идеальное интегрирующее звено с передаточной функцией

Wo{p)=f.

В соответствии с (24.7) получаем дискретную передаточную фунщию разомкнутой системы

W{z) = . (24.13)

Условие применимости формул (15.143) и (15.144) сводится здесь к тощ;, чтобы начальное значение переходной функции непрерывной части равнялось нулю, т. е. ho (0) = 0. Это будет выполняться в том слчае, когда степень числителя передаточной функции непрерывной части Wo (р) меньше степени знаменателя.

Как и в импульсных системах, условием устойчивости замкнутой системы будет \ Zi <: 1, где Zj -корни характеристического уравнения (15.158):

1 -1- (z) = 0.

Точность системы может определяться по коэффициентам ошибок (15.171), а быстродействие и запас устойчивости - построением переходного процесса или частотными методами (см. главу 15).

На основании изложенного можно представить структурную схему системы регулирования с ЦВМ следуюпщм образом. Вне зависимости от сложности решаемых математических задач можно считать, что ЦВМ оп-ределяет разность между необходимым значением регулируемой вели- У . ® чины и действительным значением.

Определим условие устойчивости замкнутой системы. ,Характеристиче- ское уравнение системы 1 + (z) = О приобретает вид

Z-1 + кт = о:

Для вьшолнения условия <С 1 необходимо, чтобы удовлетворялось неравенство

КТ<2. (24.14)

Это и будет условием устойчивости системы.

Если необходимо иметь запас устойчивости, то можно воспользоваться для его оценки, например, понятием показателя колебательности. Найдем дискретную частотщгю передаточную функцию, положив z = е . В результате получаем

W (z)

. КТ аТ

Нетрудно видеть, что амплитудно-фазовая характеристика представляет собой прямую, параллельную оси мнимых (рис. 24.5). Условие получения заданного показателя колебательности

M+i

(24.15)

Это условие дает допустимое соотношение между обпщм коэффициентом усиления К, который в рассматриваемом случае, как нетрудно показать,

равен добротности по скорости Kq, и периодом повторения ЦВМ.

Построим переходный процесс при подаче на вход ступенчатого воз-

Рис. 24.5.

2Т ЗТ Рис. 24.6.

действия g (i) = 1 (г). Дискретная передаточная функция замкнутой системы

izrgw- (24.16)

Изображение единичной ступенчатой функции будет (табл. 15.1)

(24.17)

G(2) = Z11(()1 = .

Изображение выходной величины

F(z) = 0(z)(z)=-3:.

(24.18)

Примем следагющие значения произведения добротности по скорости иа период повторения:

1) КТ = 1,4, что соответствует М = 1,5;

2) КТ = 1, что соответствует М = 1 для максимального значения КТ;

3) КТ = 0,5, что соответствует М = I.

Раскладывая (24.18) в ряд Лорана, получаем значения выходной величины у [пТ\ в дискретные моменты времени, соответствующие п = О, 1, 2, . . . Процессы изображены на рис. 24.6. Значения выходной величины в дискретные моменты времени соединены между собой прямыми линиями, соответствующими переходньш характеристикам интегрирующего звена, которьш является непрерьшная часть системы.

Нетрудно заметить, что оптимальный процесс будет при М = i (случай 2). Тогда переходный процесс длится конечное время, равное одному периоду повторения.

Пример 2. Рассмотрим систему с астатизмом второго порядка. Пусть передаточная функция непрерывной части имеет вид

Ио(р)=+---

В соответствии с (24.9) получаем

W{z) = -

(£-1)2

(24.19)

Воспользуемся для расчета методом логарифмических частотных характеристик. Для этой цели применим подстановку (15.162) и перейдем к г;-цре-образованию

(24.20)

Для перехода к частотной передаточной функции сделаем подстановку т

= j-X, где % представляет собой абсолютную псевдочастоту. В резуль-

тате получим частотную передаточную функцию

:(l-t-M)(l-/-f я)

*(-)=-

Модуль этой величины

W* (А) =

и фаза

Ki/i-i-XHy 1+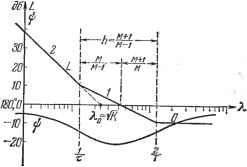

ф = -180° + arctg тХ-arctg

Рис. 24.7.

По этим выражениям на рис. 24.7 построены асимптотическая л. а. х. и л. ф. X. Нетрудно} видеть, что этот случай по расположению фазовой характеристики сводится к случаю л. а. х. типа 2-1-2, изображенной на рис. 12.13. Используя полученные в главе 12 формулы, получаем требуемую протяженность участка с наклоном 20 дб/дек в оптимальном случае:

Базовая частота л. а. х. Яо = /7Г.

Далее, имеем связь между постоянной времени т и базовой частотой: