ных процессов в цепи якоря динамика двигателя описывается двумя уравнениями, определяющими равновесие э. д. с. в цепи якоря:

и равновесие моментов на валу двигателя:

где и - напряжение, прикладываемое к якорю, и - коэффщиенты пропорциональности между обратной э. д. с. и скоростью вращения Q и между вращающим моментом и током якоря i, J - приведенный момент инерции, L ж R - индуктивность и сопротивление цепи якоря.

Переходя в обоих уравнениях к операторной форме записи и решая их совместно, получим передаточную функцию двигателя постоянного тока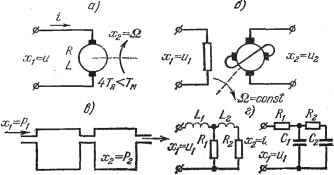

Рис. 4.16.

при управлении напряжением якоря как отношение изображений скорости двигателя и напряжения якоря:

(4.31)

где 7,

= J - электромеханическая постоянная времени двига-

теля, = J - электромагнитная постоянная времени якорной цепи,

Qq и Мо - скорость холостого хода и пусковой момент двигателя.

Для того чтобы корни знаменателя выражения (4.31) были вещественными и передаточную функцию можно было бы представить в форме (4.30), необходимо выполнение условия 42 м-

Переходная функция и функция веса звена приведены в табл. 4.2.

Частотные характеристики приведены в табл. 4.3. Построение асимптотической л. а. X. производится аналогично тому, как это было сделано для апериодического звена первого порядка. Вначале проводятся вспомогатель-

1 г 1

ные вертикальные линии через сопрягающие частоты со = и со

Для определенности построения принято, что Гд > Т. Л. а. X. строится по выражению

L (со) = 20 Ig I (/со) I = 20 Ig-, .

(4.32)

женньш

которому соответствует прямая с отрицательным наклоном 20 дб/дек (вторая асимптота). Для частот со > =- выражение (4.32) заменяется приближенным

L(c.) 201g-

которому соответствует прямая с отрицательным наклоном 40 дб/дек (третья асимптота). Действительная л. а. х. показана в табл. 4.3 пунктиром.. Она отличается от асимптотической в точках излома на 3 дб.

4. Колебательное звено. Звено описывается тем же дифференциальным уравнением (4.27), что и апериодическое звено второго порядка. Однако корни характеристического уравнения Тр + ГР + 1=0 должны быть комплексными, что будет выполняться при < 21.

Левая часть дифференциального уравнения обычно представляется в виде

(Г2р2 + 2L,Tp 1) = fci, (4.33)

где q = -f- - угловая частота свободных колебаний (при отсутстввш затухания), а - параметр затухания, лежащий в пределах О <; < 1. Передаточная функция колебательного звена

Примеры колебательных звеньев приведены на рис. 4.17. К ним относятся колебательные ЛЬС-цепи (рис. 4.17, а), управляемые двигатели постоянного тока при выполнении условия 47 > (рис. 4.17, б), упругие механические передачи, например для передачи вращательного движения (рис. 4.17, е), с упругостью С, моментом инерции / и коэффициентом скоростного трения S, гироскопические элементы (рис. 4.17, г) и др.

Рассмотрим для иллюстрации гироскопический элемент (рис. 4.17, г). В качестве входной величины примем момент М, прикладываемый к оси а, а в качестве выходной - угол поворота этой же оси а.

Уравнение равновесия моментов на оси

dt dt dt

Будем считать, что на оси 3 (оси прецессии) не действуют нвскакие внещние моменты. Тогда для этой оси уравнение равновесия моментов запшпется так:

Левее первой сопрягающей частоты со < j это выражение заменяется приближенным

L (ю) л; 20 Ig fc,

которому соответствует прямая с нулевым наклоном (первая асимптота

л. а. X.). Для частот у-<< <; выражение (4.32) заменяется прибли-

в этих формулах А и В - моменты вшерции по осям а и р, Я - кинетический момент гироскопа, равный его полярному моменту вшерции /, умноженному на угловую скорость вращения Q, ж F - коэффициент скоростного сопротивления на оси а.

Переходя к операторным выражениям и рещая оба уравнения совместно, получаем:

Я2 Р I Я2

Это уравнение можно переписать следующим образом:

где f - - квадрат угловой частоты нутационных колебаний, а =

= А - параметр затухания, определяемый действием сил скоростно-

го трения на оси а. Это уравнение совпадает с выражением (4.34). Для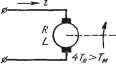

Х,=и

а;,=ос,

Моховик

Двмпсрер Рис. 4.17.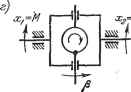

рещения дифференциального уравнения (4.33) или (4.34) необходимо найти корни характеристического уравнения

Г V-f 2?Гр-Ы =-Ь -Ь1 - 0.

Решение дает

Pi, 2 = - 7 + А = - 4- ± Т- У - = - ± ш УТ\ (4.36)

Вещественная часть корня -у представляет собой коэффициент затухания переходного процесса, а Я - частоту затухающих колебаний.

Временные характеристики звена приведены в табл. 4.2, а частотные характеристики - в табл. 4.3.

Амплитудная частотная характеристика может иметь резонансный пик. Исследование модуля частотной передаточной функции на максимум показывает, что пик будет существовать при t, < 0,707. Высота пика будет тем больше,- чем меньше параметр затухания:

Максимуму а., ч. х. соответствует частота

(4.37) (4.38)