Такая задача является типичной, например, для летательных аппаратов при ограничении угла отклонения руля и скорости его движения.

Задано: = -10 сек~, = 25 сек , Vy - 0,3 рад, == i рад/сек. Переменные коэффициенты а (t) и by (t) заданн в виде графиков (рис. 23.5). Возмущающее воздействие / (t) является случайным и описывается каноническим разложением

/ it) = wjy it) + wj, it), (23.49).

где случайные величины и имеют следующие математические ожидания и дисперсии:

М Iwy] = М [wj = 0, D [wy] = D [w\ = 0,6,

a так называемые координатные функции (i) и fit) заданы графически (рис. 23.6).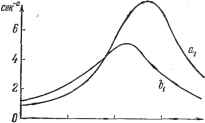

f5 3D Рис. 23.5.

45 t,ceK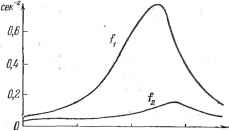

15 30

. Рис. 23.6,

t.cen

Дополнительно к этому вводятся еще ограничения на фазовые коорди наты движения объекта по траектории

Z) < 0,005, £) bj < 0,01 сж2,

а также на коэффициенты kyVikB виде

0<A;i<15, О < < 10 сек.

Ставится задача отыскания значений коэффициентов нелинейного закона управления ку, к, к, оптимизирующих систему по критерию точности (минимальная ошибка):

= imixl + mxl)dtj, (23.50)

и вторая задача - отыскания значений тех же коэффициентов, оптимизирующих систему по энергетическому критерию (минимум затраты энергии на управление):

wY\- (23.51)

Результаты решения первой задачи оптимизации описанным выше алгоритмическим методом, проведенного на ЦВМ, даны в табл. 23.1.

В этой таблице показано не только как меняются значения самих коэффициентов ку, к, kg на каждом шаге последовательной оптимизации, но и то, как меняется, постепенно уменьшаясь, дисперсия ошибки (отклонения объекта) D [ху] в конце управляемого движения {t = tt), а также и величина минимизируемого функционала If

Решение второй задачи оптимизации - по энергетическому критерию (23.51) - приводит к следующим результатам (табл. 23.2).

Таблица 23.2

Из таблицы видно, что коэффициенты к, к, kg нелинейного оптимального закона в этом случае существенно отличаются от первого в основном за счет увеличения коэффициента kg при кубическом члене выражения нелинейной функции (23.47) и уменьшения коэффициента к. Видно также, что точность управления при минимизации затраты энергии ухудшается.

В заключение отметим, что описанным здесь методом последовательной оптимизации на базе нелинейного программирования с использованием ЦВМ могут решаться задачи синтеза оптимальных систем большой сложности, в том числе многомерных, с уравнениями высокого порядка и с произвольными видами внешних воздействий и налагаемых практикой ограничений при различных критериях оптимальности.

Таблица 23.1

РАЗДЕЛ V

ЦИФРОВЫЕ И АДАПТИВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

ГЛАВАМ 24

СИСТЕМЫ РЕГУЛИРОВАНИЯ С ЦИФРОВЫМИ ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ

§ 24.1. Общие понятия

Использование цифровых вычислительных машин (ЦВМ) для управления автоматизированными объектами имеет большие перспективы. Это объясняется значительньши вычислительными и логическими возможностями ЦВМ, что позволяет реализовывать сложные алгоритмы управления.

Включение цифровой вычислительной машины в систему автоматического регулирования требует рассмотрения двух групп вопросов.

К первой группе относятся вопросы, связанные с проектированием и реализацией самой ЦВМ, а также ее входных и выходных устройств (преобразователей), задачей которых является преобразование непрерывных физических величин к цифровому виду и обратно.

Ко второй группе относятся вопросы, связанные с изучением влияния дискретного характера выходных сигналов ЦВМ на динамические свойства системы автоматического регулирования. Дальнейшее изложение будет касаться именно этой группы вопросов.

Как правило, целесообразно вводить ЦВМ в систему регулирования в тех случаях, когда требуется сложная обработка поступающей информации. Так, например, в системах управления движущимися объектами необходимо производить сложные вычисления, связанные с операциямипре-образования координат, решение прямоугольных и сферических треугольников, счисление пути и т. п. В системах управления сложными производственными объектами, например доменньши печами, автоматизированньши линиями ИТ. п., приходится производить большой объем логических операций.

Ввиду сравнительно большой сложности ЦВМ включение ее в состав автоматизированной системы оправдывается тогда, когда на ЦВМ возлагается решение ряда задач с обслуживанием нескольких зависимых или независимых каналов управления.

Общий случай системы регулирования с ЦВМ изображен на рис. 24.1. Здесь gy, g-g, is, . . gn представляют собой задаюпще воздействия, в функции которых ЦВМ вырабатывает регулируюпще воздействия, прикладываемые к системе регулирования; у, у, г/д, . . ., г/ являются регулируемыми величинами, а fy, f, fsj > fm - возмущающими воздействиями.

По своему принципу действиям ЦВМ является вычислительнымустрой-ством дискретного действия. Поэтому и система регулирования с ЦВМ представляет собой дискретную систему.

Ввиду того, что рассмотрение системы со многими переменньши (рис. 24.1) представляет собой весьма громоздкую задачу, ограничимся случаем, когда ЦВМ вводится в одиночный контур регулирования с одной регулируемой