В отличие от примера 1, здесь процесс регулирования может идти не с одним переключением, а с несколькими, в зависимости от начальных условий.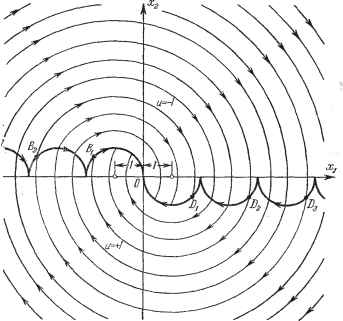

Рис. 23.4.

Итак, искомое уравнение преобразовательной части системы и =а и (х) будет

и{х) =

+1 ниже линии BzBiODiDDg и на полуокружности D,0, - 1 выше линии BsBiODiDDs и на полуокружности Bfi.

(23.33)

Поскольку Xl = X, 2 = то указанная линия переключения представляет собой определенну10 зависимость

(23.34)

вследствие чего уравнение преобразовательной части системы можно, представить в прежнем виде (23.26), но с новым значением Устройство

измерительно-преобразовательной части системы, согласно этому нелинейному закону регулирования, будет здесь аналогично прежнему (пример 1), но с другим алгоритмом вычислений.

Замечания. Сделаем некоторые общие замечания для оптимальных по быстродействию систем с линейной стационарной заданной частью без внешнего воздействия. В обоих примерах рассматривались системы второго порядка. Для них были получены линии переключений. Для систем высокого порядка будут получаться поверхности переключения в многомерном фазовом пространстве. При этом, если заданная часть системы п-го порядка

имеет только вещественные неположительные корни (включая нулевые), то процесс будет иметь не более п - 1 переключений, а если имеются комплексные (включая чисто мнимые) корни, то переключений может быть и больше, в зависимости от начальных условий.

Оптимальная по быстродействию система имеет релейный переключающий элемент, управляемый с помощью специального вычислительного логического устройства, алгоритм работы которого тем сложнее, чем вьппе порядок системы. При этом требуется непрерывно измерять все п фазовых координат или же, иначе,- регулируемую величину и п - 1 ее производных для введения в вычислительное устройство. Для систем высокого порядка это далеко не всегда реально. Поэтому практически прибегают к созданию не строго оптимальных систем, а систем, близких к оптимальным, но проще реализуемых. Некоторые конкретные рекомендации по таким системам см. в книге [61], стр. 474-477.

§ 23.3. Последовательная оптимизация на базе нелинейного программирования

Изложим этот метод, следуя В. М. Пономареву [105]. Рассмотрим более общий случай системы, описываемой нелинейными уравнениями динамики

iixu ...,Xn,t) + bi(t)ui-\-U{t) {i=i,...,n) (23.35)

с переменными коэффициентами, с внешними воздействиями Д- (if), которые могут иметь случайную природу при заданном распределении, и с начальными условиями

Xi = Xi при t = !f , (23.36)

которые также могут быть случайными с заданным распределением. Рассматривается конечное время процесса управления

Нужно найти оптимальный нелинейный закон регулирования

щ = щ (ху, . . ., Хп, t) (i = 1, . . ., п), (23.37)

при котором осуществляется минимум функционала (критерий оптимальности)

I = М1Н [ху, . . ., Хп, uy, . . ., Un, t], (23.38)

где М обозначает математическое ожидание, причем должоны еще удовлетворяться необходимые ограничения на некоторые переменные и характеристики, обусловленные практической реализа:цией системы.

Представим нелинейные функции q)j, Ui, Н в виде степенных рядов степени I. Заданные функции q)j будут

Фг = ciiiXi ащХп Н- ацп+1ос[ + aun+iyXix +

... 4- ttigXi ... xi+ + airxl (i= 1, ..., n), (23.39)

где величина индексов q и г определяется порядковым местом этих членов в ряде.

Аналогично и искомый нелинейный закон регулирования представляется в виде

щ = kiiXi + ... -f kinXn + kun+i->x\ + Ji(n+2) Ж1Ж2 -(-...

...-\-kiqXi ... Xi+ ...+kirXl (i=l, ...,n). (23.40)

Тогда задача оптимизации сводится к отысканию значений коэффициентов кц.

Если подставить выражения (23.39) и (23.40) в исходные уравнения, системы (23.35), то неизвестные коэффициенты kij войдут как параметрьг: в правые части уравнений системы. Поскольку решения дифференциальных уравнений являются непрерывными функциями от параметров то неизвестные Xi могут быть представлены в виде

= Xi (kij, t) (i = 1, . . /г; 7 = 1, . . г),. Л.С23.41)

Подставляя (23.41) в (23.40), получаем

Щ = щ {kij, О {i=i, п; 7 = 1, . . г). (23.42)

Аналитические выражения для функций {к, t) можно получить например, решая уравнения системы методом последовательных приближений.

Подставляя выражения (23.41) и (23.42) в формулу (23.38), получим критерий оптимальности в виде

/ = / {kij) ( = 1, . . ., п; 7 = 1, . г). (23.43)

Поскольку ограничения приводятся к аналогичному виду, то задача оптимизации нелинейного закона регулирования в общем случае сводится к задаче нелинейного программирования, т. е. к задаче отыскания минимума нелинейной функции п X г переменных при нелинейных ограничениях.

Метод последовательной оптимизации предусматривает замену полученной задачи нелинейного программирования последовательностью задач квадратичного программирования. Три возможных способа построения такой последовательности предложены в главе II книги [105]. Алгоритмы для решения задач квадратичного программирования отработаны достаточно хорошо. Один из наиболее удобных алгоритмов предложен Билом.

. При реализации метода последовательной оптимизации можно не отыскивать аналитические выражения для функций {к, t), так как в процессе численного решения используются только производные от критерия оптимальности и ограничений по искомьш коэффициентам к j. Способы получения этих производных рассмотрены в гл. II книги [1051.

Приведем один пример решения задачи оптимизации указанным методом..

Пример. Допустим, что имеется линейный объект второго порядка с нелинейным инерционным исполнительным органом регулятора. Этот исполнительный орган описьгеается апериодическим звеном первого порядка с насыщением скоростной характеристики. При этом динамика объекта описывается уравнениями

= X2 + f{t), (23.44)

==ai{t)xi + bUt), (23.45)

а регулятора- .

==CiU + c,F{a), (23.46)

где - .

F {а) = а + kgc, а == кх + кх. (23.47)

Вводятся ограничения на управление:

<У1, <У2- (23.48)