Требуется найти уравнение преобразовательной части системы и = и (х), чтобы система была оптимальной по быстродействию при переходе ее из произвольного начального состояния в равновесное состояние (а; = 0, = 0j. При этом на управление и наложено ограничение

м1<1.

Обозначив Xj = ж, 2 = , приведем уравнение (23.19) к исходному виду (23.4):

= u.

(23.20)

Функция Н согласно (23.14) и (23.4) здесь имеет вид

Н = рух 4- фи. (23.21)

Чтобы определить максимум Н по переменной и, надо найти g. Для этого воспользуемся уравнениями (23.16), которые в данном случае будут

откуда фх == Су, 1)52 = С2 - Cyf.

Принцип максимума (23.17), (23.18) с учетом выражения (23.21) и ограничения I I 1 дает

и = sign Фа = sign (cg - Cyt),

так как положительный максимум функции Н по переменной и будет согласно (23.21) при = -f-1, когда с - Cyt > О, и при и = -1, когда С2 - Cyt< 0. Поскольку линейная функция С2 - не более одного раза меняет знак, то в оптимальном процессе регулирования будет не более одного переключения с и = -{-1 ш& и = -1 или наоборот.

Следовательно, оптимальная по быстродействию система будет релейной, но не обычной релейной, а с особьш специальным законом переключения реле по знаку вспомогательной функции Фг = 2 - it- Чтобы представить себе это нагляднее, изобразим процесс на фазовой плоскости.

Исключив из уравнений (23.20) dt, получим при и = +1 дифференциальное уравнение

dxy = Xg dxi, откуда фазовая траектория будет

Рис. 23.2.

(23.22) (23.23)

Аналогично при li = - 1 получаем

Это - параболы, симметричные относительно оси абсцисс Ху.

Процесс должен заканчиваться в начале координат (ж = ж = О,

dx \

Ж2 S = О) . Поэтому сначала изобразим фазовые траектории (параболы),

вливающиеся в начало координат соответственно при и - -f-1 и при и = -1, как показано сплошньпии линиями на рис. 23.2.

Нанесем теперь и все остальные параболы с различными значениями с в формулах (23.22) и (23.23) до точек их вливания в изображенные ранее две ветви параболы, идущие к началу координат. Это и сделано на рис. 23.3. Как видим, из произвольной точки Mq (жщ! го) процесс идет по некоторой параболе MJ) при управляющем сигнале li = -1 (в другой области было бы

и = 4-1)- В точке D происходит переключение реле на сигнал и = после чего процесс идет по параболе /)С и заканчивается в точке О за конечное время, которое согласно принципу максимума является минимальным из всех возможных для перехода данной системы из состояния Мо (жю, Жао) в равновесное состояние О (О, 0).

Точка переключения реле D может находиться в любом месте кривой АОВ. Последняя называется поэтому линией переключения На ней лежат заключительные отрезки фазовых траекторий, приходящие в начало координат.

Итак, искомое уравнение преобразовательной части системы (оптимальной по быстродействию) будет

Ч-1 ниже линии АОВ и на дуге АО,

(23.24)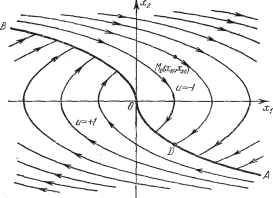

Рис. 23.3.

I --1 выше линии АОВ и на дуге ОВ,

причем ж = ж отсчитывается на оси абсцисс. Замечая, что = из формул (23.22), (23.23) и рис. 23.2 находим уравнение линии переключения:

(§)=~iSnx)2Yx, (23.25)

и следовательно, уравнение преобразовательной части системы будет

и (х) =

dx It

<

( dt )

dx I при-= (

и при

ax It

(23.26)

Ж И для

Итак, в системе должны быть либо два измерителя либо один измеритель ж и дифференцирующее устройство. Должно формироваться (автоматически вьгаисляться) переключающее значение согласно формуле (23.25), и на основе сравнения фактического текущего значения со значением (-г) , зависяпщм от текущего ж, должно производиться вклю-

\dt I п

чение и переключение реле в соответствии с уравнением (23.26).

Это является специальным нелинейньш законом регулирования для линейного объекта (23.19), приводящим к оптимальной по быстродействию системе. Таков результат решения простейшей задачи оптимизации.

Пример 2. Пусть задана система

£ + ж=и. (23.27)

Требуется найти такое уравнение преобразовательной части системы и - и (ж), чтобы система была оптимальной по быстродействию, т. е. в кратчайшее время приходила бы в равновесное состояние ж = О, = 0. При этом задана область допустимых значений управления

Перепишем заданное уравнение (23.27) в виде

1 = - §=-1 + - (23-28)

Функция Н согласно (23.14) и (23.4) здесь будет

Н = фжа -f- ф2 (-Ж1 -f- и). (23.29)

Для вспомогательных переменных из (23.16) и (23.29) получаем уравнения

откуда

г)2 = Су sin (t - Cg)-

Принцип максимума (23.17) и (23.18), с учетом выражения (23.29) и условия I W i 1, дает

и - sign ijjg = sign [sin (if - Cg)], (23.30)

так как согласно (23.29) положительный максимум величины И по переменной и будет при и = если фа > О, и при и = -1, если фа < 0. При и = 4-1 уравнения системы (23.28) будут

-2, .--Ж14-1.

Решения их имеют вид

ж = 1 - а cos (t -f Р), Жа = G sin (if 4- p),

где G О, 0 P < 2л;. Следовательно, фазовые траектории при и = +1 будут окружностями

(ху - 1)2 -1- ж = а\ (23.31)

Ана-погично при и = -1

{ху + 1)2 -1- = (23.32)

Очевидно, что вливающиеся в начало координат фазовые траектории будут иметь вид полуокружностей (23.31) и (23.32) с радиусами а = i (рис. 23.4). Это будут концевые участки траекторий. В них будут входить в произвольных точках By и Dy предыдущие участки фазовых траекторий снизу (где и = 4-1) в виде полуокруншостей с центром, смещенньш на единицу вправо (DzBy), а сверху (где и = -1) - с центром, смещенньш на единицу влево [BDy). Это будут именно полуокружности, так как знак и меняется согласно (23.30) через t = п. Следовательно, линия переключения составится из единичных полуокружностей, как показано на рис. 23.4 в виде ломаной кривой ByODyDDs-