в результате находим . .

а = щУЩ1, (22.39)

где согласно приложению 2

Перейдем теперь к уравнению (22.38) для регулярной составляющей, т. е. для полезного сигнала х. Функция F определяется в нем графиком

рис. 22.6, б в зависимости от х = -т- и Оу = . В начальной части все кривые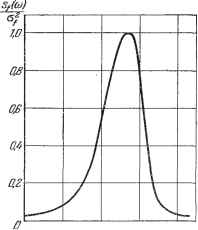

2ff 40 ео

Рис. 22.11.

80 ы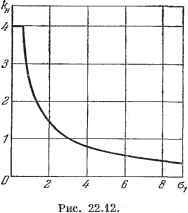

этого графика близки к прямым. Поэтому можно провести их обычную линеаризацию в виде

F = k, (22.41)

где - крутизна в начале координат (рис. 22.6, б), которая зависит от величины Оу. Для данной задачи получим

Физически величина является коэффициентом усиления полезного сигнала в нелинейном звене в присутствии помех, причем приведенная таблица дает зависимость этого коэффициента от уровня помехи, т. е. от

среднеквадратичного ее значения Oi = , на входе нелинейного звена.

Как видим, увеличение уровня помехи ведет к существенному снижению коэффициента усиления полезного сигнала в нелинейном звене, что показано графически на рис. 22.12. Это составляет принципиальную особенность нелинейной системы, которая обусловливает зависимость всех ее статических и динамических качеств по полезному сигналу, в том числе и устойчивости, от уровня помех.

Найдем, например, зависимость устойчивости системы от уровня помех. Для этого согласно. (22.38) и (22.41) запишем характеристическое уравнение системы:

ТР + + kJiocKp + кккТ + ккоК = 0. (22.42)

Условие устойчивости системы по критерию Гурвица принимает вид

(22.43)

При заданных в начале параграфа параметрах это дает к > 1,17. Это согласно рис. 22.12 соответствует значению

Но согласно (22.39)

где обозначено

сг,=--2,65.

(22.44)

Эту величину удобно принять для выражения среднеквадратичного значения внешней помехи Uf в относительных единицах, учитывая, что согласно рис. 22.10 размерности переменных f {t) ш х связаны между собой именно через коэффициент к = kjc,-

Вычислив величину Ig по формуле (22.40) при заданных выше параметрах системы, из (22.44) находим

Это означает, что только при уровне помех, не превышающем указанного значения, данная система остается устойчивой. Далее она теряет устойчивость по полезному сигналу.

а} 1Б

и ав

20 40 60 ВО К О Q2 0,4 0,6 0,8 Tj

Рис. 22.13.

Выясним теперь влияние параметров и па устойчивость системы в присутствии помех. Для этого по формуле (22.43) найдем сначала границы устойчивости системы на плоскостях параметров к, к и Т, ку (рис. 22.13, а

и б). На границе устойчивости для каждого значения по графику рис. 22.12 {mm по приведенной выше таблще) находим величину о, а по ней согласно (22.44) и среднеквадратичное значение внешней помехи, при которой теряется устойчивость системы:

Of Oi

(22.45)

Это позволяет перестроить найденные на рис. 22.13 границы устойчивости в новые координаты соответственно

и Ti,

(рис. 22.14, а и б). При этом надо иметь в виду, что величина /д, согласно (22.40), зависит от параметра Т, вследствие чего вычисление по формуле

0,03

ПД5 ОМ

20 40

о,оз

о,сг

БО 80 л

Рис. 22.14.

04 0,Б

(22.45) при построении графика рис. 22.14, б необходимопроизводить с учетом изменения /д при изменении Ту.

Как видим, с увеличением параметра к опасный уровень помех снижается, а при увеличении параметра Ту он растет. Это вполне естественно, поскольку Ту является, согласно рже. 22.10, коэффициентом интенсивности введения производной, улучшающим стабилизацию системы.

По линейному уравнению, вытекающему из (22.38) и (22.41),

\Рг (Тр -Ы) -Ь (ЙАосР + kkjyp + Мо) U = О,

используя линейную теорию автоматического регулирования, можно исследовать также и все другие динамические качества данной нелинейной системы по полезному сигналу в присутствии помех, учитывая, однако, при этом все время, что величина коэффициента зависит от уровня помехОу, от общей структуры и от некоторых параметров системы.