так как здесь математические ожидания ж и F представляют собой смещения центра случайных составляющих.

Когда функция смещения (22.28) найдена, ее можно подставить в уравнение (22.17):

Q{p)x + R{p)0{x)=S{p)f{t), (22.29)

и отсюда по заданной функции / (Q найти путем решения дифференциального

уравнения регулярную составляющую процесса ж (f).

В большинстве задач функция смещения (22.28) будет иметь вид плавной кривой (рис. 22.9), которую в некоторых пределах можно подвергнуть обычной линеаризации

= /СнЖ, K--{pi =tgp. (22.30)

В. случае, если система такова, что линейная часть с передаточной функцией

Л{Р)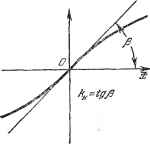

Рис. 22.9.

Q{P)

не пропускает спектр частот, соответствующий флуктуациям () и определяемый спектральной плотностью Sj (со), отыскание величины о. значительно упрощается, а именно из (22.21) следует

Ч-оо

2я \

Sf (со) ск),

(22.31)

т. е. Ох не будет зависеть от формы нелинейности и от величины ж.

В этом случае вместо дифференцирования функции смещения (22.28) можно определить kg непосредственно ) из (22.27):

F - kx, кг,= {\~ .

Здесь kj, получается как функция от а:

кп = к{ах).

(22.32) (22.33)

Затем надо подставить величину a, найденную из формулы (22.31).

Вместо этого можно воспользоваться кривой на рис. 22.3, б - 22.6, б, соответствующей найденному значению о- При этом вычисление интеграла (22.31) производится по готовым формулам ст = й/ (см. приложение 2).

В результате подстановки (22.30) или (22.32) уравнение для определения регулярной составляющей (22.29) станет линейным:

[Q {р) + kR {р)]х S{p) fit).]

(22.34)

Оно решается при помощи обычного характеристического уравнения

Q{p)+ kR (р) = 0. (22.35)

) Графически это будет тангенс угла наклона кривых на рис. 22.3, б - 22.6, б для соответствующих нелинейностей.

Важно отметить, однако, следующее. Согласно формулам (22.21) и (22.31) величина сТж зависит от спектральной плотности помехи Sf (со). Поэтому и определяемая через величину Ох форма функции смещения (22.28) и крутизна ее (рис. 22.9) зависят не только от параметров самой системы, но также и от спектральной плотности помехи Sf (со). Но если зависит от Sf (со), то согласно (22.34) и (22.35) все статические и динамические качества и даже устойчивость системы по полезному сигналу будут зависеть не только от параметров самой системы, но и от параметров спектральной плотности внешней случайной помехи. Следовательно, устойчивая при отсутствии помех нелинейная система может при определенном уровне помех потерять свои качества, т. е. выйти из строя как система автоматического управления не по причине того, что система перестает фильтровать полезный сигнал, как бывает обычно, а потому, что основной контур регулирования меняет свои динамические качества с изменением к или даже становится неустойчивым.

Возможны случаи, когда это специфическое для нелинейных систем явление будет наступать раньше, чем система, рассчитанная как линейная, перестанет фильтровать полезный сигнал. С этой точки зрения учет фактически имеющихся в системе автоматического управления нелинейностей при наличии высокочастотных (по сравнению с полезным сигналом) помех является чрезвычайно важным для практики. Это столь же важно, как и учет влияния вибрационных синусоидальных помех, рассмотренный в § 21.2. Результаты решения обеих задач аналогичны.

Очевидно, что описанное специфическое для нелинейных систем влияние помех в некоторых случаях может и улучшать динамические качества системы.

Привлекательной стороной изложенного метода является то, что исследование качеств переходных процессов, всех частотных характеристик и других качеств системы управления по полезному (регулярному) сигналу производится любыми методами линейной теории автоматического регулирования по уравнению (22.34). Несмотря на эту линеаризацию решения задачи, хорошо выявляются и все важные для практики специфические нелинейные явления благодаря описанному методу определения коэффициента кц, учитывающему несправедливость принципа суперпозиции для нелинейных систем.

Важно иметь в виду еще следующее. Исследуя методами линейной теории регулирования по уравнению (22.34) изменение статических и динамических качеств системы по полезному сигналу с изменением структуры и параметров этой системы, надо обязательно учитывать при этом и изменение самого коэффициента к, вытекающее из выражений (22.33) и (22.31) или (22.21)

§ 22.3. Пример исследования влияния случайных помех на динамику нелинейной системы

На нелинейную систему автоматического управления (рис. 22.10) действует случайная помеха / (t), являющаяся высокочастотной по сравнению

-to-

Рис. 22.10.

с медленно меняющимся полезным сигналом управления в данной системе. Проходя через нелинейное звено, помеха изменяет его коэффициент усиления

k{TiJc,+i)

d(0.

Чтобы привести этот интеграл к стандартному виду (§ 11.6), преобразуем сначала знаменатель спектральной плотности, а именно:

(of - 0)2)2 + fx22 I 2 (j£2) 2

Тогда согласно обозначениям приложения 2 получим

А (/со) = о (/ )® + ai (/tt>) + 2 + cis,

cfo = аТ a-i = -\- [iT а, = ofT, + [i, cig = cOj. В числителе же получим

G (со) = I Tja -Ы р = &осо* + Ъа + Ь

&о = 0, = Г?, &г = 1.

1) Это определяется путем простого построения амплитудной частотной характеристики линейной части системы по ее передаточной функции.

ПО отношению к полезному сигналу (вторая задача § 22.2). Требуется оценить влияние этого явления на динамические качества данной системы автоматического управления по полезному сигналу.

Уравнение замкнутой системы (рис. 22.10) в целом будет

рНТР + 1) ж + [kJcocP + kkjp + fcfco) F (ж) = kp {Тр + 1) / {t), (22.36)

где к = fcj/cg, F (ж) - заданная нелинейность (рис. 22.10, б). При этом

заданы: к = 18, к = 60, fcoc = 0,03, к = 0,5, = 0,5, = 0,02, - = 4.

Помеха имеет нормальный закон распределения и задана спектральной плотностью (рис. 22.11)

И )=(53да, (22.37)

где а = 0,05, р = 1,35, = 7,5, р, = 0,03. Меняя величину дисперсии помехи О/, характеризуюш;ую уровень помехи , будем определять динамические качества системы в зависимости от величины а.

Произведя статистическую линеаризацию (22.3), разобьем уравнение системы (22.36) на два, соответственно для регулярной и случайной составляющих:

р {ТгР +1) ж -f (/сгйосР + kkJip + kh)F = 0, I 38)

iP (Тр +1) + (fcsfcocP + yJiP + kh) cf] ж = kp (Tip + l)f{t). I

Поскольку передаточная функция линейной части системы

УУп(р)~ pS{T2P+i)

при заданных выше ее параметрах практически не пропускает ) частот, при которых спектральная плотность помехи (рис. 22.11) имеет существенное значение, тО согласно (22.31) дисперсия помехи на входе нелинейного звена будет

+ОО -f оо