I 22.2] ПРОСТЕЙШИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ 673

Далее получаем выражения типа (22.13), где 2 [/2п

Эти функции для случая т = 0,5 изображены на рис. 22.5, виг.

4. Характеристика типа насыщения (рис. 22.6, а). По формуле (22.4) с учетом обозначений (22.12) и (22.14) находим

1 fi±iФ +fizdФ ( ,)(,-и!

что показано в зависимости от Ху при разных Оу на рис. 22.6, б. По формулам же (22.9) и (22.11) находим выражение (22.13), где

<==[1-(£.у + {1-2щи)[ф{щ) + Ф{щ)- +

ф<) = [ф( ,) + ф(г,2)],

что изображено на рис. 22.6, виг.

§ 22.2. Простейшие случайные процессы в нелинейных системах

В данном параграфе рассматриваются такие задачи, в которых регу-лярнай составляющая процесса х (математическое ожидание) постоянна или медленно меняется во времени по сравнению с составляющими основных частот спектра случайной составляющей хР. Обратимся к нелинейным системам, динамика которых описывается уравнениями вида

Q{p)x+ Rip) F{x, рх) = Sip)f (t), (22.15)

где / (t) - внешнее воздействие, представляющее собой случайный процесс, причем

f{t) = J+r{t). (22.16)

Здесь / - заданное математическое ожидание (регулярная составляющая), а f - центрированная случайная составляющая.

Пусть параметры системы таковы, что автоколебания отсутствуют и система устойчива относительно равновесного состояния. Применив статистическую линеаризацию (22.3) и подставив полученное выражение в заданное уравнение (22.15), разобьем последнее на два уравнения:

Q{p)lc-\-R{p)F==S{p)i: (22.17)

[<? (Р) + R (Р) О (Р) Г, (22.18)

соответственно для регулярных (математических ожиданий) и случайных (центрированных) составляющих. При этом

F{x, ст), д (ж, ст)

определяются для каждой заданной нелинейности, как указано в § 22.1. Рассмотрим в общем виде две различные задачи.

Sf (to) da, (22.21)

где в выражении

S (ж, а,) (22.22)

необходимо X заменить найденной выше функцией (22.20). Тогда в уравнении (22.21) останется одна неизвестная величина а. Учитывая формулы (11.91) и (11.92), уравнение (22.21) можно записать в виде

ol = kIr,{x, Gf), (22.23)

где h - постоянный множитель, выносимый за знак интеграла (формулы для вычисления интеграла приведены в приложении 2).

Таким образом, путем решения уравнения (22.23) с подстановкой (22.20) будет найдено среднеквадратичное отклонение о, а затем по формуле(22.20) будет вычислено и математическое ожидание х, т. е. полностью определится искомое приближенное решение ) уравнения (22.15):

ж = жЧ-ж . (22.24)

Это решение справедливо для случая установившегося режима при стационарном случайном процессе.

Однако зависимость ж (ст) далеко не всегда можно выразить из уравнения (22.19) в явном виде ввиду сложности выражения F (ж, a). Поэтому в большинстве случаев придется решать совместно два уравнения, (22.19) и (22.23), либо численно, путем последовательных приближений, либо графически.

Можно применять, например, следующий графический прием. Представим уравнение (22.19) в виде двух уравнений:

П=ж,

5 (0) -г R (0) ,~ ,

(22.25)

Первое из них дает прямую 1 (рис. 22.7, а), а второе - серию кривых 2 для различных постоянных значений a. Перенеся все точки пересечения этих кривых с прямой 1 на плоскость координат ж, (рис. 22.7, б), получим зависимость Ux (ж) в виде кривой 3, так как каждой точке пересечения на верхней! графике соответствовало определенное значение а. После этого

1) Во всех задачах здесь и далее будем искать приближенное решение только для переменной х, стоящей под знаком нелинейности. Когда оно найдено, всегда можно через соответствующие передаточные функции найти приближенное решение и для других переменных системы.

Первая задача. Если имеет место стационарный процесс, то величины /, X, Ох являются постоянными (имеет место некоторый установившийся режим) и уравнение (22.17) принимает алгебраический вид:

Q{0)x + H (0) F {х, и) = S (0) /. (22.19)

Здесь фигурируют две неизвестные: х и о х- Поэтому в принципе отсюда можно лишь выразить величину х как функцию ct-

ж(ст). (22.20)

Далее по линейной теории случайных процессов, описанной в главе 11, производится исследование уравнения (22.18). В этом уравнении величина /я задана спектральной плотностью Sf (ш) или корреляционной функцией Tf (т). Линейная теория дает

S (/ш)

построим (рис. 22.7, б) еще одну зависимость (ж) в виде кривой 4 по формуле (22.23), подставляя в правую часть этой формулы значения о, взятые для каждого ж из кривой 3. Очевидно, что координаты точки пересечения С кривых 3 ж 4 представляют собой искомый результат совместного решения уравнений (22.19) и (22.23).

Вторая задача. Перейдем теперь к решению другой задачи, когда исследуется неустановившийся процесс.

Часто в автоматических системах управления разложению искомого решения (22.24) на и afi соответствует разложение его на полезный регулярный сигнал ж и случайную помеху х. Когда полезный сигнал управления ж изменяется во времени, процесс уже не будет стационарным. Однако, если помехи (флуктуации) характеризуются спектром значительно более высоких частот, чем полезный сигнал, можно считать последний медленно меняюш,им-ся. Тогда можно исследовать случайный процесс в первом приближении как стационарный, применяя формулу (22.23). Но при этом для определения регулярной составляющей ж нельзя пользоваться алгебраическим уравнением (22.19), а надо обращаться к дифференциальному уравнению (22.17).

В этом случае описанное выше графическое решение не годится и следует поступать иначе. Сначала надо из уравнения (22.23) определить зависимость

(ж). Для этого по аналогии с графическим решением (21.25) разобьем

уравнение [(22.23) на два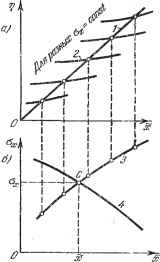

Рис. 22.7.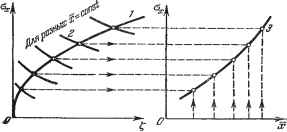

уравнения:

(22.26)

Рис. 22.8.

й/ (ж, ст)=£.

Первое из них дает параболу Т (рис. 22.8), а второе - серию кривых 2 при разных постоянных значениях ж. Перенеся ординаты их точек пересечения на плоскость ж, и отложив для

каждой из них соответствуюпще кривым 2 абсциссы ж, получим в виде кривой 3 (рис. 22.8) искомую зависимость Ох (ж).

Подставив полученную зависимость (ж) в вычисленное для заданной нелинейности согласно § 22.1 выражение

F (ж, а,), (22.27)

исключим из него величину a- и получим функцию от одной переменной

= Ф(ж), (22.28)

которую, как и в главе 19 и § 21.2, можно назвать функцией смещения ),

1) По аналогии с введенными ранее функциями смещения это будет сглаженная при помощи случайных флуктуации нелинейная характеристика для медленно меняющейся составляющей процесса.