
 |
|
|
Главная -> Логарифмическое определение устойчивости многих случаях, когда первый из этих способов дает завышенные значения корреляционной функции нелинейного процесса F (t) по сравнению с точными, второй дает заниженные значения. Поэтому часто может получиться более хорошее приближение, если в качестве величины дл взять среднее арифметическое из двух: (22.8) и (22.10). Важно иметь в виду, что величины F и д взаимосвязаны тем, что каждая из них зависит от обеих рассматриваемых характеристик случайного процесса: ж и о (входяш;их в закон распределения w). Сам факт наличия этих зависимостей и их взаимосвязь и позволяют, несмотря на линеаризацию задачи, уловить суш;ественно нелинейные особенности случайных процессов, подобно тому как в прежних главах зависимость величин F , q и q от всех 0,6 0,4 0.2 0.6 ОЛ D.Z Рис. 22.3. трех неизвестных ж , а и со (или по крайней мере от первых двух из них) и взаимосвязь этих величин позволяли исследовать суш;естБенно нелинейные особенности регулярных процессов во времени методом гармонической линеаризации. Приведем выражения величин F ntfw их графики для некоторых типовых нелинейностей, составленные по формулам (22.4), (22.9) и (22.11) при условии нормального закона распределения (22.5) случайной переменной ж (при других законах распределения величины iF п (f имели бы другие выражения). 1. Идеальная релейная характеристика (рис. 22.3, а). Из формулы (22.4) находим Р=--сФ{и), и = - где обозначено 0:.Т/2 (22.12) (числовые значения этого интеграла вероятностей имеются в справочниках, а также приведены на стр. 305). Зависимость величины F/c от отношения ж/озс показана графически на рис. 22.3, б. По формулам (22.9) и (22.11) находим соответственно (22.13) ф<1=У1-ф2(и), Зависимости ф и ф> показаны на рис. 22.3, е. У2л 2. Однозначная релейная характеристика с зоной нечувствительности (рис. 22.4, а). По формуле (22.4) с учетом обозначения (22.12) находим (22.14) Функция FIc изображена графически на рис. 22.4, б в зависимости от Ху при разных значениях о.
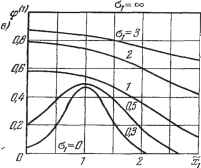
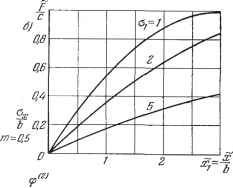
Рис. 22.4. По формулам (22.9) и (22.11) получаем выражения типа (22.13), где ,(1) что изображено графически на рис. 22.4, в ж г. 3. Петлевая релейная характеристика общего вида (рис. 22.5, а). По формулам (22.7) находим Е==\\Ф{и~Ф(иФ {щ)-Ф{и\, где кроме (22.14) и (22.12) введены еще обозначения Ш-\-Х\ -Х\ 3 = -Ь?- 4=- Зависимость Flc для случая т = 0,5 показана на рис. 22.5, б. аг о
 оа О Рис. 22.5.
2/ 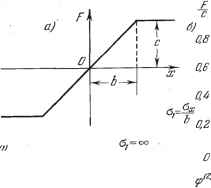 os 0,0 0.4
0.0 0,4 аг о Рис. 22.6.
= оо
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||