ГЛАВА 22

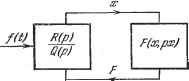Рис. 22.1.

Q{p)x + R (р) F (х, рх) S{p)f (t).

(22.1)

то схематически можно себе представить прохождение сигналов, как показано на рис. 22.1. Проходя через линейную часть, случайный процесс f (t), заданный двумя первыми вероятиостньши моментами, преобразуется в переменную X, которую тоже моишо определить двумя первыми моментами. Однако определение дальнейшего преоб!ра8ования случайного процесса х {t) в нелинейном звене F (х, рх) существенно связано с высшими вероятностными моментами (подобно тому как в главе 18 приходилось иметь дело с высшими гармониками). Ввиду замкнутости контура системы это обстоятельство накладывает отпечаток и на все процессы в данной системе. Поэтому точное решение задачи в большинстве случаев оказывается недоступным.

§ 22.1. Статистическая линеаризация нелинейностей

Предварительно заметим, что по уравнениям, выведенным в § 19.2 и в § 21.2, можно исследовать также медленно меняющиеся случайные процессы в автоматической системе, сопровождающиеся соответственно автоколебаниями и вынужденными колебаниями. При этом целесообразно функцию смещения Ф (х ) подвергнуть обычной линеаризации (19.70) и затем целиком применить линейную теорию случайных процессов к уравнению (19.73) или (21.44). Нелинейная же колебательная часть решения определяется с помощью гармонической линеаризации так же, как и в § 19.2 и в § 21.2. При этом находятся сглаженная характеристика (функция смещения) и зависимости амплитуды и частоты колебательной составляющей от величины медленно меняющейся составляющей. В этом случае предполагается, что внешние воздействия / (t) в (19.73) и Д (t) в (21.44) являются медленно меняющимися случайньши процессами с нормальным законом распределения (см. подробнее § 10.1 в книге [1001).

Для решения других задач при случайных воздействиях удобно бывает применять

так называемую статистическую линеаризацию нелинейностей, разработанную И. Е. Казаковым [491. Сущность ее заключается в следующем.

Для оценки динамической точности автоматических систем при случайных воздействиях будем определять два первых вероятностных момента случайных процессов: математическое ожидание (среднее значение) и дисперсию (или среднеквадратичное отклонение). Последнее эквивалентно определению спектральной плотности или корреляционной функции.

Если нелинейная система описывается дифференциальным уравнением

- oo -oo

которое для петлевых нелинейностей F (ж) при симметричном законе распределения (в том числе и нормальном) упрощается. Например, д.ля

Достаточно хорошее для целей инженерных расчетов первое приближение применительно к рассматриваемым классам систем, обладающих свойством фильтра (см. § 18.2), дает пренебрежение высшими моментами, т. е. замена нелинейного звена эквивалентным линейным, которое одинаково с данным нелинейным преобразует два первых вероятностных момента: математическое ожидание (среднее значение) и дисперсию (или среднеквадратичное отклонение). Это и называется статистической линеаризацией нелинейности.

Эта операция по общей идее (но не по конкретному содержанию) аналогична тому, как в главе 19 нелинейное звено при помощи гармонической лшюаризации заменялось эквивалентным линейным, которое одинаково с данным нелинейньш преобразует постоянную (или медленно меняющуюся) составляющую и первую гармонику колебательной составляющей, т. е. принимались во внимание два первых члена ряда Фурье и отбрасывались все высшие гармоники.

Итак, представим переменную х под знаком нелинейности F (х, рх) в виде

х = х + х<, (22.2)

где X - математическое ожидание (среднее значение), которое является обьшной (регулярной) функцией времени, ж яР - случайная составляющая с нулевым математическим ожиданием (центрированная случайная функция времени). Это представление аналогично тому, которое употреблялось в главе 19 при гармонической линеаризации, но оно имеет совсем другой, вероятностный смысл. Далее, и переменную F (х, рх) также представим в виде

F {х, px) = F + (fsf, (22.3)

где F - математическое ожидание (среднее значение) нелинейной функции F, которое является регулярной составляющей, (f - эквивалентный коэффициент усиления случайной составляющей (центрированной). Это выражение по форме тоже аналогично тому, которое применялось в главе 19, но имеет иное конкретное содержание.

Величина регулярной составляющей F определяется, следовательно, по известной формуле для математического ожидания. В случае однозначной нелинейной функции F (х) эта формула дает

F==M{F (х-\-х)\= j F{x+3P)iv (х) dx, {22А)

- оо

где М - обозначение операции взятия математического ожидания, w (ж) - дифференциальный закон распределения случайной составляющей, например нормальный закон (рис. 11.10):

w=-i=-e 2 U.W . (22.5)

Для нелинейности общего вида F (ж, рх) будет более сложное выражение:

4-00 -foo

F= j j F(ж--ж px + poif)w{x, px)dxdpx, (22.6)

нелинейности, показанной на рис. 22.2, будет

-bj. -оо

+ { У [1 + ) + 2 (ж + Ж )] If; (х) da; + J F (х+х ) w (х) dx. (22.7)

Величину эквивалентного коэффициента усиления q< случайной составляющей Б формуле (22.3) рекомендуется определять одним из следующих двух способов.

Первый способ исходит непосредственно из величин среднеквадратичных о.-клонений и Ор переменной х и нелинейной функции F, а именно:

- .E -,/i£j!m (22.8)

ЧТО в случае однозначной нелинейности F{x) дает

/ +00

= У F (х-Ьхя) W (х) dx-

(22.9)

Рис. 22.2.

Для общего случая (х, рх) и в случае петлевой нелинейности F (х) получаются более сложные выражения, которые можно получить для д , обобщив (22.9) по тому же образцу, как обобщены выражения (22.6) и (22.7) по сравнению с (22.4).

Второй способ заключается в определении коэффициента из условия минимума математического ожидания квадрата разности истинной нелинейной функции F (х, рх) и ее заменяющей (22.3), т. е. минимума среднеквадратичного отклонения. Записав это условие

получим

MF (х, рх) - д<х=л]2} == min.

М [(а:сл)2] (j

(22.10)

где Грх. - значение взаимной корреляционной функции переменных F w. х при т = 0. Отсюда в случае однозначной нелинейности Fx) находим

+ 00

4 J F{Z+xf)xJ4v{x)dx.

f(22.11)

Аналогично предыдущему легко получить также выражение коэффициента q< для общего случая F (х, рх) и для петлевой нелинейности F (х).

Второй способ определения коэффициента приводит к более простым расчетным формулам. С этой точки зрения его использование предпочтительнее. По точности же оба способа примерно равноценны и соответствуют общей степени приближенности всего метода в целом. Замечено, что во