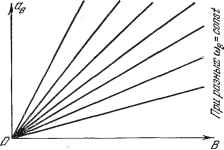И, кроме того, внешнее задаюш;ее или во8муш;аюш;ее воздействие (t), которое по отношению к помехе является медленно меняюш;имся. Уравнение динамики системы приводится к виду (21.24).

Решение уравнения (21.24) иш;ется в виде (21.26), где ж° - полезный сигнал управления, а ж* - вибрационная помеха иа входе нелинейного звена. Разбив уравнение (21.24) на два, а именно на (21.31) и (21.33), необходимо, согласно развитому выше обш;ему методу, определить сначала с по-мош;ью (21.33) и (21.29) функцию смещения = Ф (ж ), после чего можно решать дифференциальное уравнение (21.31) относительно переменной ж (i) при заданной функции Д (t). Однако в данной задаче этот общий метод решения можно упростить. Рассмотрим два случая.

В том случае, когда вся приведенная линейная часть системы (рис. 21.11), определяемая передаточной функцией

УЛр) = , (21.49)

практически не пропускает вибраций с заданной частотой в, уравнение (21.33) можно записать в виде

Тогда амплитуда вибраций на входе нелинейного звена будет определяться формулой

al= i( B)+i( B) в\ (21.50)

где через (сОв), ( в) и Xq ( в), Yq ( в) обозначены вещественные и мнимые части соответственно для выражений (/ в) и Q (/ в).

Формула (21.50) дает линейную зависимость (В) с разными коэффициентами пропорциональности для разных частот вибраций <Вв (рис. 21.12).

В частности, для схемы рис. 21.11 они будут определяться структурой линей-, ных блоков 1 ж 2.

По сравнению с общей теорией здесь существенно то, что амплитуда вибраций йв на входе нелинейного звена в этом случае не зависит от величины полезного сигнала ж . Поэтому здесь, как и в задаче 1, отпадает необходимость отыскания функции смещения Ф (ж ) и характеристика нелинейного звена по полезному сигналу (ж ) будет Рис 21 12 определяться непосредственно первой

формулой (21.29), представленной графически, например, на рис. 21.6, а. Однако здесь нужно подставить в выражение F° или взять на графике рис. 21.6, а значение а, определяемое по формуле (21.50) или графиком рис. 21.12. Поэтому, Б отличие от задачи 1, здесь даже для простейших нелинейностей очертание характеристики нелинейного звена по полезному сигналу (ж*) и ее крутизна

=( £0)0=0

будут зависеть не только от амплитуды В, но и от частоты сОв вибрационных помех, а также, конечно, и от параметров линейных блоков 1 ж2 (рис. 21.11), входящих в формулу (21.50).

Рассмотрим далее другой случай, когда первая гармоника вибраций с заданной частотой в пропускается линейной частью системы с передаточной функцией (21.49), но все же не пропускается каким-либо одним блоком системы. Пусть, например, в схеме на рис. 21.11 вибрации не пропускаются вовсе только управляемым объектом, а по внутренней обратной связи первая гармоника вибраций с частотой <Вв проходит. Тогда, вообще говоря, уже нельзя не считаться с зависимостью (21.34) амплитуды вибраций а переменной ж от величины полезного сигнала х°. Однако и в этом случае возможно упрощение решения задачи по сравнению с общей теорией, состоящее в том, что при определении функции смещения выбрасывается часть системы, не пропускающая вибраций (рис. 21.13, а).

В этом случае нужно записать уравнение динамики только оставшейся части системы (рис. 21.13, а):

Q{p)x + (р) F (ж, рж) = (р) и it) + ip) h it), (21.51)

которое будет, конечно, проще общего уравнения (21.24). Отсюда по аналогии с (21.35) получим уравнение для определения амплитуды вибраций на входе нелинейного звена в виде

(<Вв) + 1 1с(Ив)

Xi к, СОв, жО) + У? (ав, Шв, жО)

где через Xjc, 52с и Хс, обозначены вещественные и мнимые части соответственно для Sc (7®в) и для выражения

<?с (/ в) + (/ в) \.q (йв. в, ж ) + jq (йв, в, жО)1.

Написанное уравнение позволяет определить зависимость амплитуды вибраций в от величины полезного сигнала ж° на входе нелинейного звена для каждой заданной внешней

Линейное звене Z

Линейное звено J-.

Ойрат-наясвнзь

вибрационной помехи (т. е. для заданных В, <Вв) графическим приемом, описанным в § 21.2 (рис. 21.7).

Полученная зависимость a{x) подставляется затем в первую из формул (21.29) для получения функции смещения = Ф (ж°), которая Б данном случае и будет являться характеристикой нелинейного звена по полезному сигналу. Вид ее будет зависеть от заданных амплитуды В и частоты <Вв внешних вибраций и от параметров системы, входящих в выделенную часть контура (рис. 21.13, а).

В обоих рассмотренных случаях, проведя линеаризацию F = к- характеристики нелинейного звена F (ж ) или F = = Ф (ж ) по полезному сигналу,

можно обьшными методами теории автоматического регулирования, используя линейные уравнения (21.44), выявить зависимость всех статических и динамических качеств данной нелинейной системы автоматического управления (и ее устойчивости) от амплитуды В и частоты сОв вибрационных помех.

Линейная система выходила бы из строя при наличии помех тогда, когда полезный сигнал практически перестал бы различаться на фоне помех.

Рис. 21.13.

Но пока он нормально различается, все статические и динамические свойства системы по полезному сигналу, если система линейна, остаются неизменными. Вибрационная помеха при этом накладывается как дополнительная ошибка. Совсем иначе дело обстоит в нелинейной системе. Коэффициент усиления ка полезного сигнала в нелинейном звене, а вместе с ним и все качества и даже устойчивость системы могут настолько существенно зависеть от помехи (от В и в), что система может выйти из строя по этой причине раньше, чем перестанет различаться полезный сигнал на уровне помех. Это очень важно учитывать на практике.

С точки зрения упрощения решения задачи нужно всегда иметь в виду упрощенную формулу линеаризации (21.45), которая позволяет и во втором из рассмотренных случаев обходиться без определения функции смещения. В этом случае нужно подставить в (21.45) значение амплитуды вибраций на входе нелинейного звена а, найденное при отсутствии полезного сигнала (ж = 0) любым из двух методов, изложенных в § 21.1, но для более простого уравнения системы (21.51). Зависимость (В) будет при этом, в отличие от первого случая, криволинейной (рис. 21.13, б).

В заключение заметим, что тем же методом, что и в § 18.5, легко вьшис-лять высшие гармоники вынужденных колебаний (см. § 9.4 книги [1001).