расход жидкости в гидравлическом двигателе и т. п. Выходной величиной является скорость вращения Q. Дифференциальное уравнение движения при равенстве нулю момента нагрузки может быть представлено в виде

где / - приведенныйк валу двигателя суммарный момент инерции, - коэффициент пропорциональности между управляющим воздействием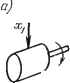

№ 1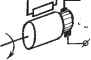

J2 =const

JO.=U,

Рис. 4.13.

и вращающим моментом, = - наклон механической характеристики,

равный отношению пускового момента к скорости холостого хода при некотором значении управляющего воздействия. Это уравнение приводится к виду

ГЛ Й , г. 7

и = kxi.

постоянная

где к = -j - коэффициент передачи звена, - -

времени двигателя. Оно полностью совпадает с (4.23).

В качестве второго примера (рис. 4.13, б) приведен электрический генератор постоянного тока, входной величиной которого является напряжение, подводимое к обмотке возбуждения щ, а выходной - напряжение якоря и.

Апериодическими звеньями первого порядка являются также резервуар с газом (рис. 4.13, в), у которого входная величина представляет собой давление перед впускным отверстием, а выходная - давление Р в резервуаре, и нагревательная печь (рис. 4.13, г), у которой входная величина - количество поступающего в единицу времени тепла Q, а выходная - температура, в печи f.

Электрические RC- и LR-цеиж в соответствии со схемами, изображенными на рис. 4.13, д, также представляют собой апериодические звенья первого порядка.

Во всех приведенных примерах дифференциальное уравнение движения совпадает с (4.23).

Переходная функция представляет собой экспоненту (табл. 4.2). Множитель 1 (t) указывает, что экспонента рассматривается, начиная с момента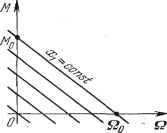

Рис. 4.14.

t = О, Т. е. для положительного времени. Во многих случаях этот множитель опускается, но указанное обстоятельство необходимо иметь в виду.

Отрезок, отсекаемый на асимптоте касательной, проведенной к кривой в любой точке, равен постоянной времени Т. Чем больше постоянная времени звена, тем дольше длится переходный процесс, т. е. медленнее устанавливается значение = kxi на выходе звена. Строго говоря, экспонента приближается к этому значению асимптотически, т. е. в бесконечности. Практически переходный процесс считается закончившимся через промежуток времени tj = ЗТ. Иногда принимают = (4 -т- 5) Т.

Постоянная времени характеризует инерционность , или инерционное запаздывание , апериодического звена. Выходное значение х = kx-i в апериодическом звене устанавливается только спустя некоторое время (п) после подачи входного воздействия.

Функция веса w (t) может быть найдена дифференцированием переходной функции h {t), и она также приводится в табл. 4.2.

Частотные характеристики приведены в табл. 4.3. Амплитудно-фазовая характеристика для положительных частот имеет вид полуокружности с диаметром, равным коэффициенту передачи к. Величина постоянной времени звена определяет распределение отметок частоты со вдоль кривой. На а. ф. х.

показаны три характерные отметки со=0, сй=фи co = ooj.A. ф. х. для

положительных частот может бьггь дополнена зеркальной полуокружностью для отрицательных частот (показана пунктиром). В результате полная а. ф. X. представляет собой окружность.

Из амплитудной характеристики видно, что колебания малых частот

со < -г) пропускаются данным звеном с отношением амплитуд выходной

и входной величвш, близким к статическому коэффициенту передачи звена к.

Колебания больших частот со > проходят с сильным ослаблением

амплитуды, т. е. плохо пропускаются или практически совсем не пропускаются звеном. Чем меньше постоянная времени Т, т. е. чем меньше инерционность звена, тем более вытянута амплитудная характеристика А (со) вдоль оси частот, или, как говорят, тем шире полоса пропускания частот АсОд у данного звена:

Ао) = 4-(4.25)

Логарифмические частотные характеристики приведены в табл. 4.3. Л. а. X. строится по выражению

- L{)=.20\g\W{j<,)\20\g-=. (4.26)

Наиболее просто, практически без вычислительной работы, строится так называемая асимптотическая л. а. х. Ее построение показано на рис. 4.15. На стандартной сетке проводится вертикальная прямая через точку с часто-

1 тт

той, называемой сопрягающей частотой со = Для частот меньших, чем

сопрягающая, т. е. при со < -у можно пренебречь вторым слагаемьгм под корнем в выражении (4.26). Тогда левее сопрягающей частоты (рис. 4.15) можно заменить (4.26) приближенным выражением L (со) л; 20 Ig А; при

со <;j, которому соответствует прямая линия, параллельная оси частот (прямая аЪ) и являющаяся первой асимптотой.

Для частот больших, чем сопрягающая {( > y) выражении (4.26)

можно пренебречь под корнем единицей по сравнению с соГ. Тогда вместо (4.26) будем иметь приближенное значение

L(co)201g-A. (присо>4-),

которому соответствует, согласно § 4.4, прямая с отрицательным наклоном 20 дб/дек (прямая be), являющаяся второй асимптотой.

Ломаная линия аЬс и называется асимптотической л. а. х. Действительная л. а. X. (показана на рис. 4.15 пунктиром) будет несколько отличаться от асимптотической, причем наибольшее отклонение будет в точке Ь. Оно

равно приблизительно 3 дб, так как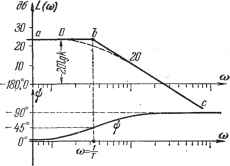

()=201g = 201g/c-3,03 дб.

что в лвшейном масштабе соответствует отклонению в /2 раз. На всем остальном протяжении влево и вправо от сопрягающей частоты действительная л. а. X. будет отличаться от асимптотической менее чем на 3 дб. Поэтому во многих практических расчетах достаточно ограничиться построением асимптотической л. а. х.

На том же рис. 4.15 показана логарифмическая фазовая характеристика. Характерными ее особенностями являются сдвиг по фазе if = -45° при сопрягающей частоте (так как arctg соГ = arctg 1 = 45°) и симметрия л. ф. х. относительно сопрягающей частоты.

3. Апериодическое звено второго порядка. Дифференциальное уравнение звена имеет вид

Рис. 4.15.

т2 2 2

- кзсщ

(4.27)

dt dt

При этом корни характеристического уравнения !Гр -Ь Тр -f- 1 = О должны быть вещественными, что будет выполняться при условии Ti!2T2-В операторной записи уравнение (4.27) приобретает вид

{Т1р + + 1) = fexi. (4.28)

Левая часть последнего выражения разлЕагается на множители:

{Т,р + 1) {Т + 1) 2 = кх, (4.29)

Гз.4 = -

Передаточная функция звена

(Р)- (1 + Гзр)(1-ЬГ4Р)

(4.30)

Апериодическое звено второго порядка эквивалентно двум апериодическим звеньям первого порядка, включенным последовательно друг за другом, с общим коэффициентом передачи h и постоянными времени и Т.

Примеры апериодических звеньев второго порядка приведены на рис. 4.16. Рассмотрим подробно случай двигателя постоянного тока (рис. 4.16, а). При отсутствии момента нагрузки на валу и при учете переход-