конкретными выражениями для F°, q ж q, приведенными в главе 19. Таким образом, для каждой конкретной нелинейности имеются готовые выражения:

F° (ж , Ов, СОв), q в, Юв), q Ов, СОв), (21.29)

причем часто величина сОв в них отсутствует. В качестве примера па рис. 21.6 приведены эти зависимости для нелинейности типа насыщения, аналогичные приведенным в главе 19.

По аналогии с [формулой (21.4) запишем

С08ф-

(21.30)

Подставив выражения для F (ж, рх), /2 (г) и ж в заданное дифференциальное уравнение нелинейной системы (21.24), получим уравнение

Q{p) (ж -fж*)-Ь?(p)(F -f

+ 2(р)(С08Ф-%)Ж*,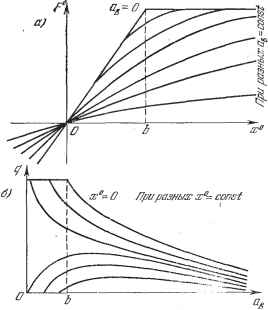

Рис. 21.6.

которое разбивается нелинейным образом (см. главу 19) на

два уравнения соответственно для медленно меняющихся и для колебательных составляющих:

Q (р) xo + R (р) FSi (р) и {Г), (21.31)

Q iP)~S, (Р) ~ (cos ф-Ы;,) ] x- + R{p)(q + -p)x = 0. (21.32)

Оба уравнения содержат все три неизвестные а, ф и х°.

Второе из этих уравнений совпадает с прежним уравнением (21.5), но только с иными коэффициентами гармонической линеаризации q ж д, зависяхцими от величины смещения ж°. Поэтому уравнение (21.32) до конца решается только совместно с уравнением (21.31), хотя, как будет видно из дальнейшего, возможны и более простые случаи. Пока же можно, написав характеристическое уравнение вида (21.12), после подстановки р = /сов привести уравнение(21.32) к следующему:

<?(/Шв)+Д(/Шв)(д+/У) . р Si (/сов)

(21.33)

в результате решения которого любым из двух методов (графическим или аналитическим), описанных в § 21.1, определяются зависимости амплитуды в и сдвига фазы ф от величины, смещения ж°, т. е.

в (ж , СОв, В), ф (ж , СОв, В), (21.34)

где х° остается пока еще неизвестным.

Для применения графического метода § 21.1 к отысканию зависимости Ов (ж ) по уравнению (21.33) нужно на рис. 21.1 построить серию кривых Z {а)

для разных значений = const, которые согласно (21.28) входят в выражения для q ж q. Уравнение аналитического метода (21.17) примет вид

XI (Ше) + У(Мв)

(21.35)

где Zg, ¥ж X,Y обозначают вещественные и мнимые части соответственно для выражения (/©в) и выражения

Q (/Юв) + R (/(Ов) Vq (ов, в, ж ) + jq (ов, в, а*)].

Уравнение (21.35) не решается так просто, как (21.17). Однако можно применить следующий графический прием его решения. Разбив (21.35) на два уравнения:

Xl{a)+Yl (СОв)

Х{щ, в, хО)-1-У{щ, йв, хО)

построим по первому из них на плоскости (, кривую 1 (рис. 21.7), а по второму - серию кривых 2 для разных значений ж = const при заданных

Рис. 21.7.

В ж ©в. Перенося полученные точки пересечения кривых вправо на плоскость получаем сразу хдакомую зависимость в (ж°) для заданного внешнего периодического воздействия, т. е. для заданной пары значений В и ©g. Эту зависимость легко получить таким же путем и для любых других заданных В и ©в.

Подставив теперь значение амплитуды в первое из выражений (21.29), найдем функцию смещения в виде

i?o = ф (а;0, еов. В), (21.36)

которая является характеристикой данного нелинейного звена системы по отношению к медленно меняющимся составляюпщм переменных F ж х. - Эти медленно меняющиеся составляющие определяются затем путем решения дифференциального уравнения (21.31), в которое надо подставить найденную функцию смещения (21.36).

Независимость очертания функции смещения Ф (ж ) от характера изменения и. места приложения медленно меняющихся внешних воздействий здесь остаётся в силе, как было и при автоколебаниях (глава 19).

Однако принципиальным отличием функции смещения (21.36), определяющей прохождение медленно меняюпщхся сигналов через нелинейную систему при наличии вынужденных колебаний, от функции смещения (19.13) при автоколебаниях является существенная зависимость ее от частоты

И амплитуды внешнего периодического воздействия (в то время как при авто-колебаниях вид функции смещения зависел только от структуры и от соотношения параметров самой системы).

В результате для каждой заданной частоты вынужденных колебаний сов получается серия кривых i = Ф {х ) для разных значений амплитуды В внешнего периодического воздействия /2 (t), как показано, например, на рис. 21.8, а. При заданных сов и Z? получается вполне определенное очертание

f=0(27%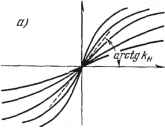

Для разных В при заданном lOg

При разных к U)g= const

/7ри задаяныа?

Рис. 21.8.

функции смещения Ф (ж ), зависящее только от структуры и параметров самой системы, входящих в уравнение (21.33).

Здесь, так же как и в главе 19, возможен и второй метод отыскания функции смещения. При этом методе попутно определяются также статические и установившиеся ошибки. Метод состоит в следующем.

Поскольку функция смещения i = Ф (ж ) не зависит от характера изменения и места приложения медленно меняющихся воздействий, то ее можно определить для простейшего случая /j = const = /J (или при астатической системе для pf const = gj). Тогда уравнение (21.31) принимает вид

Q (0) ж -Ь i? (0) Я = М ,

Slip)

(21.37) Исполь-

где М° = Si (0) /5 или для астатических систем Л/° = зуя первое выражение из (21.29), т. е. (при заданной частоте ©в)

(жо, йв), - (21.38)

из уравнения (21.37) находим

жМов, ЛГ )- (21.39)

Подставив это в выражения для g и д, определяемые второй и третьей из формул (21,29), получим зависимости

q (йв, ilf°) и д (ав, М\

Вводя их в уравнение (21.33), эквивалентное (21.32), и решая его любым из двух способов, указанных выше, при заданных S и сов находим амплитуду