Рассмотренный второй случай, когда система переходит на одночастотные колебания с частотой cOg только при В > j??nopi наблюдается чаще всего в таких нелинейных системах, которые до приложения внепшего периодического воздействия работают в автоколебательном режиме. При этом велхтаина В пор обращается в нуль в том случае, когда частота ©в совпадает с частотой автоколебаний сОц данной системы (рис. 21.3, г). Вор равно нулю обычно также в области отсутствия автоколебаний (область устойчивости равновесия системы, рис. 21.3, д).

Тогда выше кривых на рис. 21.3, г, д будут лежать значения амплитуды В внепшего воздействия, при которых существует одночастотный режим вьшужденных колебаний с частотой сОв (область захватывания), а при значениях, лежащих ниже кривой, будет иметь место более сложное вынужденное движение системы. Это и является определением (пока графическим) условий захватывания, о которых говорилось выше.

В других нелинейных системах может быть Воц = О, как в случае рис. 21.3, б.

Аналитический метод. Из равенства (21.14) или (21.15) можно получить аналитические выражения для определения амплитуды и сдвига фазы ф одночастотных вьшужденных колебаний нелинейной системы. Для этого выделим вещественные и мнимые части числителя и знаменателя и запишем равенства для модулей и аргументов обеих частей уравнения (21.14) или 21.15):

ХЧав,сОв) + УМ в.св) (21.17)

где X ж Y - вещественная и мнимая части числителя выражения (21.14) или (21.15), Xs и Ys - вещественная и мнимая части знаменателя, т. е. S (/©в)- При этом X и У соответствуют левой части заданного нелинейного уравнения (21.2), т. е. являются теми же самыми выражениями X ш Y, которые применялись при исследовании автоколебаний (§ 18.2), а Xs и Ys являются новыми выражениями, соответствующими правой части заданного нелинейного уравнения (21.2).

Как видим, выражение (21.17) может, вообще говоря, оказаться довольно сложным алгебраическим уравнением относительно Og. Однако важно то, что это уравнение содержит лишь одну неизвестную Од, которая, следовательно, так или иначе может быть определена. После этого фазовый сдвиг ф легко вычисляется по формуле (21.18). Напомним, что и при отыскании автоколебаний (глава 18) часто получалось сложное относительно а уравнение, но это не вызывало больших затруднений. Действительно, в большинстве случаев интересуются тем, как будет изменяться амплитуда вынужденных колебаний в зависимости от частоты и амплитуды внешнего воздействия, а также при изменении того или иного параметра системы. Указанные параметры могут входить в уравнение (21.17) более простым образом, чем амплитуда в- Тогда уравнение (21.17) можно будет разрешить в явном виде относительно любого из этих параметров, а затем, задаваясь разными значениями в и вычисляя по найденной формуле рассматриваемый параметр, можно построить искомые зависимости (В), (©в) или в (к) и т. п.; затем по формуле (21.18) можно также вычислить для каждого случая фазовый сдвиг ф.

Например, возможен следующий простой прием решения уравнения (21.17). Для каждой заданной частоты внешнего воздействия ©в будем задаваться разными значениями и вычислять каждый раз величину В.

По результатам этих вычислений легко строится график (рис. 21.4), который и представляет собой искомое решение уравнения (21.17).

Что касается условия захватывания, то оно может быть определено аналитически как условие существования вещественного положительного решения для в уравнении (21.17), Это условие автоматически выявится при построении графика типа рис,21.4.

Итак, получены амплитуда и сдвиг фазы ф вынужденных колебаний для переменной х, стоящей под знаком нелинейной функции. После этого можно подсчитать амплитуду и фазу первой гармоники вынужденных колебаний для любой другой переменной исследуемой системы на основании соответствующих уравнений или передаточных функций звеньев, связывающих эту переменную с переменной х.

Частотный метод. Пусть нелинейное звено в системе определяется уравнением

y = F{x). (21.19)

Находим для пего приближенную амп.питудно-фазовую характеристику Wn(a) согласно формулам (18.210) и (18.211). Рассмотрим два случая.

Первый случай. Передаточная функция - замкнутой системы

Рис. 21.4.

такова, что

i + W (ja) (a) Oo))-1-W {a)

(21.20)

гдеМл (/to) =

- обратная амплитудно-фазовая характеристика линей-

ной части. Изобразим характеристики (/со) и - W- (а) на комплексной плоскости (рис. 21.5). Амплитуда Ов вынужденных колебаний величины х

определяет точку D, а частота cog - точку Е. Из формулы (21.20) и из чертежа (рис. 21.5) находим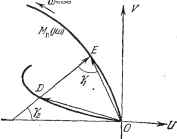

ЛГлао)в)1

В Мл(/Мв)+Ин( ) DE

откуда амплитуда В внешнего периодического воздействия / получает значение

D DE

(21.21)

Рис. 21.5. Перемещая точку Х> вдоль кривой -Wia),

можно найти зависимость величины от В при заданной частоте сОв, а перемещая точку Е - зависимость величины Ов от частоты СОв.

Второй случай. Передаточная функция ~ замкнутой системы такова, что

W (/О))

j (жо -f йв sin ф, авСОв cos ф) йф, о

J F (ж°-1-ав sinф, йвл cosф) sinф йф, о

j (Ж° -}- йв sin ф, й С0вСОбф) COS ф йф,

(21.28)

причем ф = сов + ф. Из сравнения этих формул с (19.6) видно, что при отыскании вынужденных колебаний можно целиком пользоваться всеми

Тогда на основании этой формулы и чертежа (рис. 21.5) получаем

fB 1 J

откуда

B = DE-ag. (21.23)

В других случаях, когда передаточная функция не подходит под частные виды (21.20) и (21.22), построения усложняются.

§ 21.2. Несимметричные вынужденные колебания с медленно меняющейся составляющей

Вынужденные колебания будут несимметричными в следующих случаях:

1) при несимметричных нелинейных характеристиках системы;

2) при наличии постоянного или медленно меняющегося внешнего воздействия (в статических системах);

3) при наличии постоянной или медленно меняющейся скорости изменения внешнего воздействия (в астатических системах).

В общем случае будем полагать, что к нелинейной системе приложены два внешних воздействия, вследствие чего ее уравнение вместо (21.2) имеет вид

Q{p)x + R ip) F (ж, рх) = ip) и {t) + ip) h it), (21.24)

причем /i it) - медленно меняющееся внепшее воздействие, а it) - периодическое внешнее воздействие:]

/а it) = В sin сов. (21.25)

Медленно меняющееся воздействие Д it) считается мало изменяющимся

за период Гв = - , т. е. предполагается, что возможные частоты изменения

/i it) значительно ниже частоты сОв.

Решение уравнения (21.24) будем искать в виде

ж = ж Ч- ж*, ж* = в sin (сов + ф), (21.26)

где х - медленно меняющаяся составляющая, а ж* - колебательная составляющая, амплитуда в и фаза ф которой в общем случае тоже медленно изменяются во времени.

Тогда гармоническая линеаризация нелинейности F (ж, рх) может производиться по формуле, аналогичной (19.5):

/ (ж, рж) = .РО-Ьдж*--рж*, (21.27)