ПЯв J

q=~ { F {asSini, аввсосф) sinij) йф, о

F ( в sin ф, йвЕ COS ф) COS ф йф,

(21.8)

ф = ЮвМ- Ф, (21.9)

где искомыми неизвестными постоянными будут амплитуда и сдвиг фазы ф, в то время как частота сов здесь уже задана выражением (21.1). В отличие от такой типичной постановки задачи можно будет, конечно, в дальнейшем решать и обратную задачу определения потребной частоты в или аьшлитуды В внешнего воздействия по заданной амплитуде вынужденных колебаний и т. п.

Чтобы иметь возможность применить тот же обхций подход к решению задачи, который был принят при отыскании автоколебаний, выразим в уравнении (21.2) переменную / через х. Согласно (21.1)

f (t) = В sin [(сов + ф) - ф] = i? cos ф sin (сов + ф) - В sin ф cos (cogi -- ф).

Отсюда, принимая во внимание выражение (21.3) для х и выражение для его производной

рх = йвв COS (сОв + 4>)i

окончательно получаем

/()=А(ео8ф-р)х. (21.4)

Подставив это выражение в заданное дифференциальное уравнение системы (21.2), получим

Q {р)-S{р) (cos~Jp)]x +В {p)F{x, рх)=-0. (21.5)

Таким Г)бразом, неоднородное нелинейное уравнение (21.2) при заданном внешнем воздействии (21.1) и предполагаемой форме решения (21.3) сведено к однородному нелинейному уравнению (21.5), содержащему добавочный член в левой части. Уравнение (21.5) аналогично прежнему уравнению (§ 18.2) и отличается от него только заменой операторного многочлена Q (р) на новый операторный многочлен, стоящий в (21.5) в квадратных скобках. Применяя при отыскании синусоидального периодического решения формально тот нее метод, что и в главе 18, нужно потребовать выполнения свойства фильтра от этой новой системы.

Заданная нелинейность F (ж, рх) должна допускать симметричные колебания, т. е. должно выполняться условие

F{assini, as<ihicos) dt = 0. (21.6)

Итак, получив для определения вынужденных колебаний однородное уравнение (21.5), можно, как и в § 18.2, произвести гармоническую линеаризацию нелинейности

F{x, px)==qx + jpx, (21.7)

что, однако, не влияет на результат вычисления q и q. Поэтому при определении симметричных однозначных вынужденных колебаний можно целиком пользоваться готовыми выражениями для qnq, приведенными в главе 18, с заменой в них а, (о на а, сов- Таким образом, для каждой нелинейности Б общем случае получаются зависимости

q (йз, сОв), q ( в, Юв), (21.10)

;а во многих частных случаях (см. главу 18) -

д(йз), д;(йв). (21.11)

В результате из (21.5) и (21.7) получаем характеристическое уравнение .для первого приближения

Q{p)~-S(p)[cos(f~p)+R{p)[q + p)-=Q. (21.12)

Подставляя сюда чисто мнимое значение р = /соц, что соответствует .отысканию синусоидального решения (21.3), получаем

Q (7 в) - S (7©в) - (cos ф у sin ф) -Ь i? (/©в) (д + iq) = 0. (21.13) Замечая, что

cos ф - 7 sin ф = е~, зиз уравнения (21.13) находим, что

S (/(Ов)

(21.14)

Возможны два метода дальнейшего решения задачи. Эти методы остаются справедливыми и для нелинейных систем с временным запаздыванием т,

когда выражение (21.14) принимает вид

g(/coB)+(/coB)(g+/gV- -g,-,-, (21.15) л (;сОв)

или другой аналогичный вид, содержащий т.

Графический метод. Для каждого значения частоты при заданных параметрах системы на комплексной плоскости строится кривая (рис. 21.1)

Z (а,) = g(/b)+(/o3e)(g+/g). (21.16)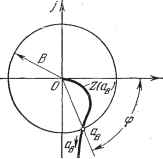

Рис. 21.1.

Эта кривая соответствует левой части равенства (21.14) 1). Правая же часть (21.14) изобразится в виде окружности радиуса В. Пересечение ее с кривой Z (йз) дает решение задачи, причем в точке пересечения по дуге окружно--сти определяется фазовый сдвиг ф, а по кривой Z (а) - величина амплитуды йз вынужденных колебаний.

Зависимость амплитуды вынужденных колебаний йв от частоты ©в (рис. 21.2, б) мончно получить, если на рис. 21.1 начертить серию кривых 2, (йв) при раз1п.1х постоянных значениях сОв (рис. 21.2, й). Таким же путем.

1) Аналогично решается задача и в случае выражения (21.15).

строя кривые Z {а при разных постоянных значениях какого-нибудь параметра h (рис. 21.2, а), можно определить зависимость Og от любого параметра системы к (рис. 21.2, е), входящего в выражение (21.16) для 2 ( в)-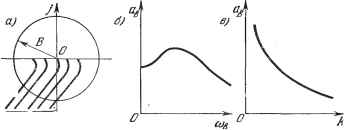

Лриразных

Рис. 21.2.

Для отыскания зависимости от амплитуды внешнего воздействия В нужно нанести серию концентрических окружностей разных радиусов В (рис. 21.3, а). При этом возможны два случая: 1) когда имеется точка пересечения окружности с кривой Z ( в) при любой величине радиуса В, начиная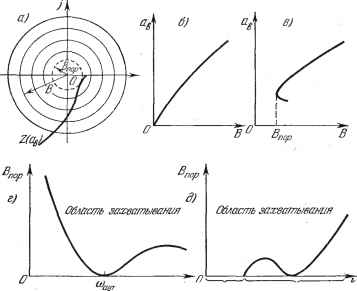

Область Область авто-ycmouvmocTu т/1ебаиий равноввсля

Рис. 21.3.

от нуля, что дает зависимость (В), например, в виде рис. 21.3, б; 2) когда точка пересечения окружности с кривой Z (а) существует только при значениях радиуса В, превышающих некоторое пороговое значение Вор (рис. 21.3, а), что приводит к зависимости (В) типа рис. 21.3, в.

Графетеское определение Snop ясно из чертежа. Можно построить зависимость пороговой амплитуды В внешнего воздействия от частоты сОв при заданных параметрах системы (рис. 21.3, г) или от любого параметра к при данной частоте сОв (рис. 21,3, д). Последнюю зависимость можно найти с помощью рис. 21.3, а, построенного для серии кривых Z (ов), соответствующих разлхтаным к.