В ЭТОМ случае отрицательное влияние постоянной времени т (а) ском-пенсируется введением дополнительного демпфирования с помощью слагаемого 2 I с I РЧ>-

Аналогичными приемами можно стабилизировать запас по фазе, показатель колебательности и т. п., т. е. исключить плавание этих характеристик из-за нелинейности при изменении величины сигнала.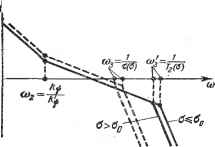

i20lg\W(Joj,(£}\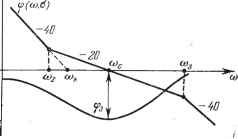

Рис. 20.26.

Рис. 20.27.

Обеспечение повышенной точности внешнего контура. Поставим задачу выбора структуры и параметров блока Wi (рис. 20.23), обеспечивающего устойчивость внешнего контура и повышенную точность стабилизации величины Z с учетом ранее выбранной структуры и параметров первого и второго контуров.

Передаточная функция промежуточного контура по отношению к управляющему воздействию будет

W (p, a)

Если рассматривать наиболее характерные частоты, влияющие на работу внешнего контура, т. е. о < ©сг то получим

:<1.

Тогда

W (р. О)

Oz or)

(20.84)

В случае линейной системы блок И , имеет структуру (20.74), а блок Wz внешнего контура должен иметь следующую структуру:

(р) = т,{1 + Т,р), причем по рекомендации линейной теории

Tz = nTa, mi =

kTz VTzTa

(20.85)

(20.86)

где n - некоторое число, выбор которого зависит от требований к колебательности и запасу по фазе внешнего контура.

Зависимость установившейся ошибки z-t от возмущений /г и fy опре-.деляется формулой

(20.87)

Для уменьшения установившейся ошибки ZyT при ранее выбранном ку необходимо увеличивать т-у. Однако предельное значение ограничено требованием обеспечения устойчивости системы.

Для уменьшения установившейся ошибки можно рекомендовать нелинейный закон регулирования, на-

пример, в виде

= 2.1 I Z Г sign Z 4- mz. (20.88) Тогда

W,(p,z)= = miz)ll+Tiz)p],

(20.89)

m{z)=ml\z\-, Т {z) =

m(z)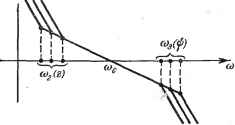

Передаточная функция разомкнутого внешнего контура

в (Р, Z, If) - 2 Рис. 20.28.

(20.90)

На рис. 20.28 представлены логарифмические алшлитуднхе частотные характеристики, соответствующие этой передаточной функции. Характерно, что частота среза (о Ti данном случае не зависит от величины сигнала z. Характеристика 1 соответствует малым сигналам, а. S - большим сигналам.

Величина установившейся ошибки в данной системе будет

bc. = [kih + h]- (20.91)

Расчеты и моделирование показывают, что таким путем можно в несколько раз повысить установившуюся точность по сравнению с линейным законом регулирования при сохранении устойчивости и требуемых запасов по фазе я по амплитуде.

ГЛАВА 21

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ

§ 21.1. Симметричные одночастотные вынужденные колебания

Проблема определения вынунеденных колебаний нелинейных систем вообще является весьма сложной и многообразной. Поскольку принцип наложения решений (суперпозиция) здесь несправедлив, то, вообще говоря, нельзя складывать частные решения при различных внешних воздействиях, найденных по отдельности, а также складывать свободные и вынужденные колебания. Особое нелинейное слонение решений возможно в случае, если решения разделяются по степени медленности протекания их во времени (т. е. по значению возможных частот колебаний), аналогично тому, как это делалось в главе 19. При этом каждое из складываемых решений существенно зависело от другого, а именно амплитуда автоколебаний существенно зависела от величины смещения, характеризующей медленно протекающие процессы. Такого же рода разделение решений для вынужденных колебаний будет рассмотрено нинсе, где появится возможность рассмотрения нелинейных двухчастотных колебаний с большой разностью частот.

Не касаясь сложных форм вынужденных колебаний нелинейных систем (хотя их исследование также имеет большое практическое значение), ограничимся в данном параграфе определением одночастотных вынужденных колебаний, когда колебания системы происходят с частотой внешнего периодического воздействия. Форма колебаний, как и прежде, на основании свойства фильтра будет считаться близкой к синусоидальной для переменной х, стоящей под знаком нелинейной функции. При рассмотрении вьшужденных колебаний во многих случаях возникают ограничения, накладываемые на амплитуду и частоту внешнего периодического воздействия (зависящие также и от параметров системы) и обусловливающие существование одно-частотных вынужденных колебаний в нелинейной системе. Будем их кратко называть условиями захватывания (в указанном широком смысле). Особое значение эти условия приобретают для автоколебательных систем при частотах, близких к частоте автоколебаний и выше.

Итак, пусть имеется некоторая нелинейная автоматическая система, в любом месте которой приложено внешнее синусоидальное воздействие

f{t)=B sin (21.1)

Пусть уравнение динамики системы приведено к виду

Q (р) X + R [р) F (х, рх) = S{p)f (t). (21.2)

Вьшолнение условий фильтра (§ 18.2), а также выводимых ниже условий захватывания (где это необходимо) позволяет в первом приближении искать решение для установившихся вынужденных колебаний системы в синусоидальной форме

X = йз sin ((Ое! + ф), (21.3)