§ 20.4] ПРИМЕНЕНИЕ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК

усиления амплитуды в виде

к{а) =

F{a)

Большое его практическое преимущество состоит в простоте вычисления к по виду F (х) и обратно, что затруднено в гармонической линеаризации. Строго говоря, это выражение к {а) соответствует не синусоидальным, а прямоугольным колебаниям (рис. 20.22), где действительно А = к{а) а (прямоугольная линеаризация). Однако вычисления показывают, что значения к (а) ж q (а) для многих типовых нелинейностей отличаются друг от друга всего на несколько процентов, что вполне приемлемо для приближенных инженерных расчетов.

Проиллюстрируем метод исследования на примере системы с нелинейным законом регулирования, формируемым Б нелинейных блоках

ж (рис. 20.23), при учете нелинейности рЬ = F (о) в виде ограничения по скорости исполнительного привода. Система имеет три контура: внутренний контур 1, промежуточный контур 2, внешний контур 3.

Параметры внутреннего контура и объекта управления заданы. Задача состоит в отыскании структуры и параметров нелинейных блоков промежуточного и внешнего контуров, т. е. нелинейных передаточных функций FF

Рис.Г20.22.

ТпрадляемыЛ объект ~\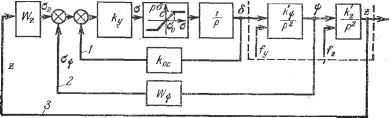

Рис. 20.23.

и Wzi обеспечивающих наилучшие характеристики управления величинами ф и Z в смысле устойчивости, а также точности стабилизации z при воздействии на систему возмущений fy ж f.

Передаточная функция внутреннего контура тоже будет нелинейной:

т(о)

%{c)p+i

(20.72)

При этом с увеличением сигнала о (при о > Oq) значение постоянной времени т (о) увеличивается.

Передаточная функция разомкнутого промежуточного контура для рассматриваемого примера будет

(20.73)

Если внутренний контур работает в линейной зоне (т. е. при а Oq), то по линейной теории регулирования рекомендуется выбрать структуру блока в виде

ТФ (р) = /1 (1 + Т,р),

(20.74)

причем, на основании требований к быстродействию и к величине перерегулирования,

Та = пГо, fci= , , (20.75)

где п - некоторое число, выбор которого зависит от того, какой коэффициент колебательности и запас по фазе необходимо обеспечить, а Tq - постоянная времени рулевого тракта при а o, т. е.

kyfCQQ

При выборе параметров регулятора по формулам (20.75) частота среза cOg будет лежать на ветви логарифмической амплитудно-частотной характеристики с наклоном в 20 дб/дек, посредине участка (, -) шириной Ig п декад.

\ а То /

Однако при а > Оо внутренний контур будет работать в зоне насыщения скоростной характеристики и постоянная времени т (а) будет увеличиваться с увеличением а. Это может привести при выбранных выше параметрах ш. ki к значительной колебательности и даже потери устойчивости в случае, когда

т (а) > Та. (20.76)

Поэтому для обеспечения устойчивости при а > o необходимо брать значения п завышенными, но тогда окажутся неудовлетворительными характеристики стабилизации при а Oq, т. е. невозможно обеспечить хорошую

настройку системы регулирования с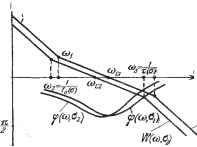

помощью постоянных k-i и Та для

всех режимов. В таком случае вместо (20.74) целесообразно вводить нелинейный закон регулирования, при котором параметры блока И.ф i будут зависеть от величины сигнала.

Стабилизация фазовой характеристики. За счет влияния нелинейности F (а) внутреннего контура на-Що>,б,) блюдается зависимость частотных 2 Л характеристик не только от частоты со (как в линейных системах), но и от амплитуды сигнала на входе а. В результате амплитудная и фазовая частотные характеристики будут плавать с изменением амплитуды а, как показано на рис. 20.24 для некоторых двух значений Oi и о. Условие стабилизации фазовой характеристики можно записать в виде

Рис. 20.24.

§ 20.4] применение логарифмических частотных характеристик 645

Передаточной функции (20.73) соответствует выражение для фазовой характеристики

ср (со, о) = - Jt + arg И , (/со, о) - arctg т (о) со. (20.78)

[arctgT(a)co]=--A ,

где .

7 СО

h = r-i-

Поэтому условие стабилизации фазовой характеристики (20.77) принимает вид

J-[arg Wija, а)] =.j-

arg (/ , о) = arctg. (20.79)

Отсюда, взяв нелинейную передаточную функцию в виде

(р, о) = kl (о) + к (о) p + ks (о) р\ (20.80)

получим условия

h (о)

kl (а) кз(о)

= Г + т(о), I

= ГаТ(0). J

(20.81)

(20.82)

ki(C)

В частности, если принять /{:i = const, то

(а) = /С1 [Та + Т (о)] = Й2 + /CiT (о),

/сз (о) = kiTat (G) = fegT (а).

На рис. 20.25 представлена схема соответствующего нелинейного блока с передаточной функцией

Видно, что при значении (о) < (о) можно с достаточным приближением реализовать стабилизацию фазовой характеристики.

На рис. 20.26 изображена л. а. х. разомкнутого промежуточного контура, построенная по передаточной функции

W (р, а) =

рПт(а)р+1][Г2(а)р+1]

(пунктиром показана характеристика Рис. 20,25.

без учета нелинейного корректирующего контура), а на рис. 20.27 изображены стабилизированные за счет нелинейной коррекции амплитудная и фазовая характеристики данной нелинейной системы для промежуточного контура 2 (рис. 20.23).

Можно рекомендовать иной способ стабилизации фазовой характеристики, используя управляющую функцию вида