В тех случаях, когда требуется значительно скомпенсировать во время переходного процесса отрицательное влияние инерционности двигателя, необходимо ввести упреждение 7 (рис. 20.19). у

Графики коэффициентов гармонической линеаризации и эквивалентных значений постоянной времени и коэффициента усиления звена для подобного типа корректирующих сигналов приведены на рис. 20.20, а, б, в при разных значениях 7.

Из рис. 20.20, в виден эффект уменьшения инерционности приводного двигателя за счет описанной коррекции.

Для оценки влияния нелинейных корректирующих сигналов рассмотрим процессы в следящей системе, схема которой изображена на рис. 20.17.

Перед усилителем следящей системы (или в первых каскадах усилителя) установлено логическое устройство, которое включает корректирующий сигнал.

В те интервалы времени, в которые знаки анализируемых

Рис. 20.19.

2,0 3.0 Рис. 20.20.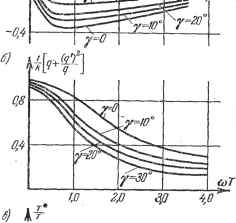

сигналов С/ и Q не совпадают, в системе формируется корректирующий сигнал, который сдвигается на время т и подается для выключения сигнала ошибки.

Уравнения системы имеют вид

6=01-62, f7i=A;i6,

С7,=.

l-hr*P

e2=-Q.

(20.66)

Отсюда выражение для ошибки системы с учетом выражений (20.59) будет - 9 {а, о)

со(7 (а, (О)

(Ц-71/) + Л

q(a, (i>)+ , -г- е а, со) J

1+ -7 р (од (а, (й)

9 (а, (о) +

д (а, (й)2 g (а, (О) .

-рВ,. (20.67)

Характеристическое уравнение системы будет

tog (а, (о)

Ti -g( . 0J)

2 = -

1 + сзз

g (а, (О) -

д (а, (0)2 9 (а, ) J

- g(a, со) у cog (й, (О) *

-дКсо)

cog (а, со)

(20.68)

Для определения автоколебаний и устойчивости воспользуемся коэффициентным методом (§ 18.2). По критерию Гурвица (4i-a - -3=0) находим критический коэффициент усиления

(од (я, (о)

причем уравнение для частоты колебаний систеьш получает вид

(20.69)

(20.70)

* cog (а, (о)

Решение системы этих двух уравнений целесообразно производить методом последовательных приближений.

Производя вычисления для заданных значений параметров системы Ту = 0,04 сек, Гг = 0,02 сек, Агд = 1, с = 5-Ю е-сек/град, = 200 град!сек -в, у = 30°, попучизм:

кар = 255 ceк , со = 75 ceк~.

В линейной следящей системе (без нелинейной коррекции) кр при таких же параметрах значительно ниже.

Для определения качества переходных процессов используем формулы (20.32) и (20.33), что дает

(од(й, ш)

L Ti -д (а, со) J

2 Tig (а. со) cog (а, со) ..

ю2 = .

- д (я, со)

cog (я, со)

yig (я, (О) cog (я, со)

Решая эти уравнения методом последовательных приближений для значения коэффициента усиления системы кт = 300 сек, получим значение показателя затухания и частоты колебаний: = -5,25 ceк, со = = 55 ceк~. Длительность переходного процесса здесь составляет примерно 0,5 сек, а перерегулирование - 74%.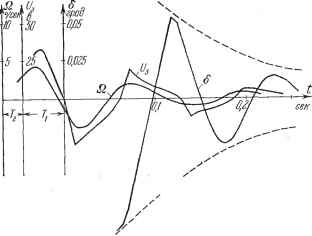

- Огибающая переходного процесса

Рис. 20.21.

Точное значение коэффициента затухания = -9 сек~ отличается от приближенного = - 7 сек~ в данном случае на 22%. Точное значение частоты колебаний сот = 52 сек отличается от приближенного значения (о = 54 сек~ на 4%. Подобная точность определения параметров переходного процесса монсет считаться вполне приемлемой.

При наличии в системе дополнительной нелинейности типа насыщения что практически почти всегда имеет место, величина первого перерегулирования существенно уменьшается.

§ 20.4. Применение логарифмических частотных характеристик для исследования нелинейных законов регулирования

Аппарат логарифмических частотных характеристик является простым расчетным средством линейной теории регулирования. Многие расчеты нелинейных систем, основанные на гармонической линеаризации нелинейностей, могут быть также переложены на язык логарифмических частотных характеристик. Однако, имея в виду желательность наибольшей простоты расчета, будем здесь вместо гармонического коэффициента усиления q (я) применять эквивалентный коэффициент усиления нелинейного звена к {х):

F {х) = к (ж) X, тр,е к (ж) =

(20.71>

Р* -1 Это выражение к (ж) является точным для любой заданной точки графика F (ж). Требуется определить коэффициент усиления амплитуды колебаний. Вьппе он записывался в виде q (а). Теперь же введем коэффициент

Для ТОГО чтобы получить аналогичное качество переходного процесса в линейной системе без использования нелинейных динамических корректирующих сигналов, необходимо, чтобы коэффициент усиления системы был не более 90 сек~, т. е. примерно в 3 раза меньше, чем в нелинейной системе. При этом показатель затухания и частота колебаний будут равны: t, = = -5 сек , (О = 40,5 сек~. Длительность переходного процесса в данном случае будет равна tfs::; 0,6 сек.

На рис. 20.21 приведены результаты точного решения исходных нелинейных уравнений для следуюпа;их значений параметров системы: kik, - 2000 kg = l,k= 200 град/сек-в, к = Ю , с = О, = 0,04 сек, = 0,02 сек.